题目内容
 如图,BD是△ABC的外角∠ABP的角平分线,DA=DC,DE⊥BP于点E,若AB=5,BC=3,则BE的长为( )
如图,BD是△ABC的外角∠ABP的角平分线,DA=DC,DE⊥BP于点E,若AB=5,BC=3,则BE的长为( )分析:过点D作DF⊥AB于F,根据角平分线上的点到角的两边的距离相等可得DE=DF,再利用“HL”证明△BDE和△BDF全等,△ADF和△CDE全等,根据全等三角形对应边相等可得BE=BF,AF=CE,再用AB、BC表示出AF、CE,整理即可解得.
解答:解:如图,过点D作DF⊥AB于F,
∵BD是∠ABP的角平分线,
∴DE=DF,
在△BDE和△BDF中,
,
∴△BDE≌△BDF(HL),
∴BE=BF,
在△ADF和△CDE中,
,
∴△ADF≌△CDE(HL),
∴AF=CE,
∵AF=AB-BF,
CE=BC+BE,
∴AB-BF=BC+BE,
∴2BE=AB-BC,
∵AB=5,BC=3,
∴2BE=5-3=2,
解得BE=1.
故选C.
∵BD是∠ABP的角平分线,
∴DE=DF,
在△BDE和△BDF中,
|
∴△BDE≌△BDF(HL),

∴BE=BF,
在△ADF和△CDE中,
|
∴△ADF≌△CDE(HL),
∴AF=CE,
∵AF=AB-BF,
CE=BC+BE,
∴AB-BF=BC+BE,
∴2BE=AB-BC,
∵AB=5,BC=3,
∴2BE=5-3=2,
解得BE=1.
故选C.
点评:本题考查了角平分线的性质,全等三角形的判定与性质,作辅助线构造出两对全等三角形是解题的关键,也是本题的难点.

练习册系列答案
相关题目
 25、如图,BD是△ABC的角平分线.已知∠1=∠A,∠2=∠3,求△ABC的各个内角的度数.
25、如图,BD是△ABC的角平分线.已知∠1=∠A,∠2=∠3,求△ABC的各个内角的度数. 如图,BD是∠ABC的平分线,DE⊥AB于E,DF⊥BC于F,AB=12,BC=15,S△ABD=36,则S△BCD=
如图,BD是∠ABC的平分线,DE⊥AB于E,DF⊥BC于F,AB=12,BC=15,S△ABD=36,则S△BCD=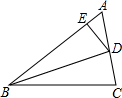 如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=90,AB=18,BC=12,求DE的长.
如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=90,AB=18,BC=12,求DE的长. 如图,BD是△ABC的角平分线,且BD=BC=AD.
如图,BD是△ABC的角平分线,且BD=BC=AD. 如图,BD是△ABC的中线,若△ABD的面积是10,则△ABC的面积是
如图,BD是△ABC的中线,若△ABD的面积是10,则△ABC的面积是