Question

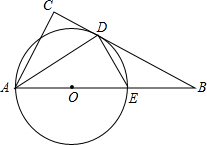如图，Rt△ABC，∠C=90°，∠CAB的角平分线AD交BC于点D，过点D作DE⊥AD，交AB于点E，以AE为直径作⊙O．求证：BC是⊙O的切线．

Answer 1

证明：如图，连接OD，
∵AE为直径作⊙O，
∴∠ADE=90°，
∴D点在⊙O上．
∴OD=OA．
∴∠ADO=∠DAO．
又∵∠CAB的角平分线AD交BC于点D，
∴∠CAD=∠DAO．
∴∠CAD=∠ADO．
∴AC∥OD，
∵∠C=90°．
∴∠ODC=90°．
所以BC是⊙O的切线．
分析：首先证明D点在圆上，则OD为半径，再证明OD⊥BC．
点评：掌握证明直线是圆的切线问题转化为证明直线垂直问题．熟练运用平行线的性质和直径所对的圆周角是直角．