题目内容
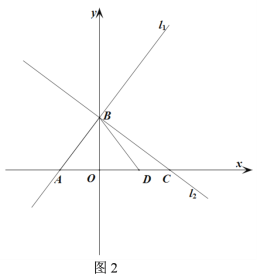
【题目】如图,直线![]() :
:![]() 与x轴、y轴分别交于A、B两点,直线
与x轴、y轴分别交于A、B两点,直线![]() 与x轴、y轴分别交于C、
与x轴、y轴分别交于C、![]() 两点,且
两点,且![]() ︰
︰![]() ︰
︰![]() .
.
(1)求直线![]() 的解析式,并判断
的解析式,并判断![]() 的形状;
的形状;
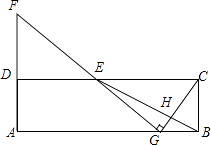
(2)如图![]() ,
,![]() 为直线
为直线![]() 上一点,横坐标为
上一点,横坐标为![]() ,
,![]() 为直线
为直线![]() 上一动点,当
上一动点,当![]() 最小时,将线段
最小时,将线段![]() 沿射线
沿射线![]() 方向平移,平移后
方向平移,平移后![]() 、
、![]() 的对应点分别为
的对应点分别为![]() 、
、![]() ,当
,当![]() 最小时,求点
最小时,求点![]() 的坐标;
的坐标;
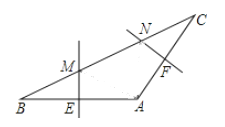
(3)如图![]() ,将
,将![]() 沿着
沿着![]() 轴翻折,得到
轴翻折,得到![]() ,再将
,再将![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() (
(![]() )得到
)得到![]() ,直线
,直线![]() 与直线
与直线![]() 、
、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() .当
.当![]() 为等腰三角形时,请直接写出线段
为等腰三角形时,请直接写出线段![]() 的长.
的长.

【答案】(1)![]() ,
,![]() 为直角三角形 ;(2)
为直角三角形 ;(2)![]() (
(![]() ,
,![]() );(3)
);(3)![]()
![]() ,
,![]()
【解析】
(1)解直角三角形求出AB、AC、BC理由勾股定理的逆定理即可解决问题;
(2)如图1中,作QM⊥x轴于M,首先说明当P、Q、M三点共线,且PM⊥x轴时,PQ+![]() CQ最小,构建一次函数理由方程组确定交点Q的坐标即可;
CQ最小,构建一次函数理由方程组确定交点Q的坐标即可;
(3)分四种情形分别求解即可解决问题;
(1)∵直线![]() :
:![]()
∴![]() (
(![]() ,
,![]() ),
),![]() (
(![]() ,
,![]() )
)
∴在![]() 中,
中,![]()
∵![]() ︰
︰![]() ︰
︰![]()
∴![]()
∴在![]() 中,
中,![]()
即![]() (
(![]() ,
,![]() )
)
设直线![]() :
:![]() (
(![]() )
)
∴![]() 解得
解得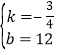
∴直线![]() :
:![]()
∵![]() ,
,![]() ,
,![]()
∴![]()
∴![]() 为直角三角形
为直角三角形
(2)作![]() 轴于
轴于![]() ,则
,则![]() ∽
∽![]()
∴![]()
∴![]() 即
即![]()
∴![]()
∴当![]() 、
、![]() 、
、![]() 三点共线,且
三点共线,且![]() 轴时,
轴时,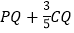 最小
最小
∴![]() (
(![]() ,
,![]() )
)
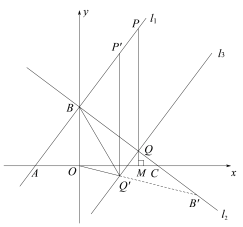
平移过程中,点![]() 在直线
在直线![]() 上移动
上移动
∵![]() 且
且![]() 经过点
经过点![]() (
(![]() ,
,![]() )
)
∴![]() :
:![]()
作点![]() (
(![]() ,
,![]() )关于
)关于![]() 的对称点
的对称点![]() ,则
,则![]() (
(![]() ,
,![]() ),连接
),连接![]() ,与直线
,与直线![]() 的交点即为所求点
的交点即为所求点![]()
∵直线![]() :
:![]()
∴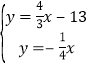 解得
解得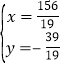
∴![]() (
(![]() ,
,![]() )
)
(3)![]()
![]() ,
,![]()

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目