题目内容
 如图,有一个△ABC,三边长为AC=6,BC=8,AB=10,沿AD折叠,使点C落在AB边上的点E处.
如图,有一个△ABC,三边长为AC=6,BC=8,AB=10,沿AD折叠,使点C落在AB边上的点E处.(1)试判断△ABC的形状,并说明理由.
(2)求线段CD的长.
分析:(1)利用勾股定理得的逆定理判断得出即可;
(2)设CD=x,则DE=x,BD=8-x在Rt△BDE中,则DE2+BE2=BD2,进而求出即可.
(2)设CD=x,则DE=x,BD=8-x在Rt△BDE中,则DE2+BE2=BD2,进而求出即可.
解答: 解:(1)△ABC是直角三角形,理由如下:
解:(1)△ABC是直角三角形,理由如下:
在△ABC中,∵62+82=102,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠C=90°;
(2)∵△ADE是△ADC沿直线AD翻折而成,
∴∠C=∠DEB=90°,CD=DE,AC=AE=6,
设CD=x,则DE=x,BD=8-x,
在Rt△BDE中,∵DE2+BE2=BD2,
∴x2+42=(8-x)2,
∴x2+16=64-16x+x2,
∴x=3,即CD长为3.
 解:(1)△ABC是直角三角形,理由如下:
解:(1)△ABC是直角三角形,理由如下:在△ABC中,∵62+82=102,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠C=90°;
(2)∵△ADE是△ADC沿直线AD翻折而成,
∴∠C=∠DEB=90°,CD=DE,AC=AE=6,
设CD=x,则DE=x,BD=8-x,
在Rt△BDE中,∵DE2+BE2=BD2,
∴x2+42=(8-x)2,
∴x2+16=64-16x+x2,
∴x=3,即CD长为3.
点评:此题主要考查了翻折变换的性质以及勾股定理和勾股定理的逆定理等知识,根据已知表示出DE,BD的长利用勾股定理得出是解题关键.

练习册系列答案
相关题目
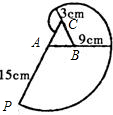 如图,有一个边长为6cm的正三角形ABC木块,点P是边CA的延长线上的点,在A、P之间拉一条细绳,绳长AP为15cm.握住点P,拉直细绳,把它全部紧紧缠绕在△ABC木块上(缠绕时木块不动),若圆周率取3.14,点P运动的路线长为( )(精确到0.1cm)
如图,有一个边长为6cm的正三角形ABC木块,点P是边CA的延长线上的点,在A、P之间拉一条细绳,绳长AP为15cm.握住点P,拉直细绳,把它全部紧紧缠绕在△ABC木块上(缠绕时木块不动),若圆周率取3.14,点P运动的路线长为( )(精确到0.1cm)| A、28.3cm | B、28.2cm | C、56.5cm | D、56.6cm |
 27、如图,有一个三角形ABC,三边为AC=6cm,BC=8cm,AB=10cm,沿AD折叠,使点C落在AB上的点E处,求线段CD的长.
27、如图,有一个三角形ABC,三边为AC=6cm,BC=8cm,AB=10cm,沿AD折叠,使点C落在AB上的点E处,求线段CD的长. 如图,有一个直角三角形ABC,两直角边AC=6cm,BC=8cm,AD平分∠BAC,点E在斜边AB上且AE=AC.
如图,有一个直角三角形ABC,两直角边AC=6cm,BC=8cm,AD平分∠BAC,点E在斜边AB上且AE=AC.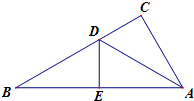 如图,有一个△ABC,三边长为AC=6,BC=8,AB=10,沿AD折叠,使点C落在AB边上的点E处.
如图,有一个△ABC,三边长为AC=6,BC=8,AB=10,沿AD折叠,使点C落在AB边上的点E处.