题目内容
 计算
计算(1)计算:2-1-
| 3 |
| 1 |
| 2 |
(2)先化简,再求值:
| 1 |
| x-3 |
| x3-6x2+9x |
| x2-2x |
| 1-x |
| 2-x |
(3)如图,梯形ABCD中,DC∥AB,点E是BC的中点,连结AE并延长与DC的延长线相交于点F,连结BF,AC.求证:四边形ABFC是平行四边形.
分析:(1)分别进行负整数指数幂、特殊角的三角函数值、零指数幂、绝对值的运算,然后根据实数的运算法则计算即可;
(2)先化为最简,然后把x=-6代入求值即可;
(3)证明△FCE≌△ABE,得出AE=FE,从而可得出结论.
(2)先化为最简,然后把x=-6代入求值即可;
(3)证明△FCE≌△ABE,得出AE=FE,从而可得出结论.
解答:(1)解:原式=
-
×
+1+
=-1;
(2)解:原式=
•
-
=
+
=-
,
当x=-6时,
代入得:-
=-
=-
;
(3)证明:
∵点E是BC的中点,
∴CE=BE,
∵DC∥AB,
在△FCE与△ABE中:
,
∴△FCE≌△ABE(ASA),
可得:AE=FE,
∵CE=BE,
∴四边形ABFC是平行四边形.
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
(2)解:原式=
| 1 |
| x-3 |
| x(x-3)2 |
| x(x-2) |
| 1-x |
| 2-x |
=
| x-3 |
| x-2 |
| 1-x |
| 2-x |
=-
| 2 |
| x-2 |
当x=-6时,
代入得:-
| 2 |
| x-2 |
| 2 |
| 6-2 |
| 1 |
| 2 |
(3)证明:
∵点E是BC的中点,
∴CE=BE,
∵DC∥AB,
在△FCE与△ABE中:
|
∴△FCE≌△ABE(ASA),
可得:AE=FE,
∵CE=BE,
∴四边形ABFC是平行四边形.
点评:本题考查了梯形、分式的化简求值及实数的运算,涉及的知识点较多,注意各知识点的掌握是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
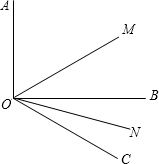 (1)如图所示,∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数.
(1)如图所示,∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数.