题目内容
（2012•乐山模拟）如图，一系列“黑色梯形”是由x轴、直线y=| 3 |
4
| 3 |
4
，Sn=| 3 |
8
n-4
| 3 |
| 3 |
8
n-4
．| 3 |
| 3 |
分析：根据图形和题意利用梯形的面积公式可以分别可以求出S1、S2、S3、S4的面积，再观察其规律就可以求出其结论．
解答：解：由图象及直线的解析式可以得出这些阴影部分的图形是梯形，
∵他们的交点在y=
x上，
∴这些梯形的两底分别是：
，3
，5
，7
，9
，11
，13
…（2n-1）
．
∴S1=
=4
=4
+0，
S2=
=12
=2×4
+1×4
，
S3=
=20
=3×4
+2×4
，
S4=
=28
=4×4
+3×4
，
S5=5×4
+4×4
，
…
Sn=n×4
+（n-1）×4
=8
n-4
．
故答案为：4
，8
n-4
．
∵他们的交点在y=
| 3 |
∴这些梯形的两底分别是：
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
∴S1=
(
| ||||
| 2 |
| 3 |
| 3 |
S2=
(5
| ||||
| 2 |
| 3 |
| 3 |
| 3 |
S3=
(9
| ||||
| 2 |
| 3 |
| 3 |
| 3 |
S4=
(13
| ||||
| 2 |
| 3 |
| 3 |
| 3 |
S5=5×4
| 3 |
| 3 |
…
Sn=n×4
| 3 |
| 3 |
| 3 |
| 3 |
故答案为：4
| 3 |
| 3 |
| 3 |
点评：本题试一道一次函数的综合试题，考查了梯形的面积公式的计算，计算中寻求解答结论的规律，找到规律是解答本题的突破点．
练习册系列答案
相关题目
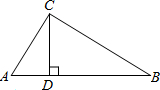（2012•乐山模拟）如图，在Rt△ABC中，∠C=90°，两直角边AC、BC的长恰是方程x2-4x+2=0的两个不同的根，则Rt△ABC的斜边上的高线CD的长为（ ）