题目内容
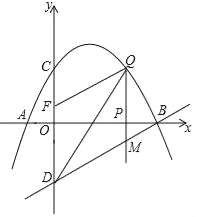
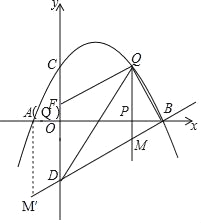
【题目】如图,已知抛物线经过点A(﹣1,0),B(4,0),C(0,2)三点,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线交抛物线于点Q,交直线BD于点M.
(1)求该抛物线所表示的二次函数的表达式;
(2)点P在线段AB上运动的过程中,是否存在点Q,使得△BOD∽△QBM?若存在,求出点Q的坐标;若不存在,请说明理由.
(3)已知点F(0,![]() ),点P在x轴上运动,试求当m为何值时以D、M、Q、F为顶点的四边形是平行四边形.
),点P在x轴上运动,试求当m为何值时以D、M、Q、F为顶点的四边形是平行四边形.
【答案】(1)y=﹣![]() x2+
x2+![]() x+2;(2)存在,点Q的坐标为(3,2);(3)m=﹣1或m=3或m=1+
x+2;(2)存在,点Q的坐标为(3,2);(3)m=﹣1或m=3或m=1+![]() 或1﹣
或1﹣![]() 时,四边形DMQF是平行四边形.
时,四边形DMQF是平行四边形.
【解析】
(1)根据待定系数法求解可得;
(2)利用△BOD∽△QBM得![]() ,再证△MBQ∽△BPQ得
,再证△MBQ∽△BPQ得![]() ,解之即可得此时m的值.
,解之即可得此时m的值.
(3)先利用待定系数法求出直线BD解析式为y=![]() x-2,则Q(m,-
x-2,则Q(m,-![]() m2+
m2+![]() m+2)、M(m,
m+2)、M(m,![]() m-2),由QM∥DF且四边形DMQF是平行四边形知QM=DF,据此列出关于m的方程,解之可得.
m-2),由QM∥DF且四边形DMQF是平行四边形知QM=DF,据此列出关于m的方程,解之可得.
(1)由抛物线过点A(﹣1,0)、B(4,0)可设解析式为y=a(x+1)(x﹣4),
将点C(0,2)代入,得:﹣4a=2,
解得:a=﹣![]() ,
,
则抛物线解析式为y=﹣![]() (x+1)(x﹣4)=﹣
(x+1)(x﹣4)=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)如图所示:
∵当△BOD∽△QBM时,
则![]() ,
,
∵∠MBQ=90°,
∴∠MBP+∠PBQ=90°,
∵∠MPB=∠BPQ=90°,
∴∠MBP+∠BMP=90°,
∴∠BMP=∠PBQ,
∴△MBQ∽△BPQ,
∴![]() ,
,
∴![]() ,
,
解得:m1=3、m2=4,
当m=4时,点P、Q、M均与点B重合,不能构成三角形,舍去,
∴m=3,点Q的坐标为(3,2);
(3)由题意知点D坐标为(0,﹣2),
设直线BD解析式为y=kx+b,
将B(4,0)、D(0,﹣2)代入,得:![]() ,
,
解得: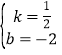 ,
,
∴直线BD解析式为y=![]() x﹣2,
x﹣2,
∵QM⊥x轴,P(m,0),
∴Q(m,﹣![]() m2+
m2+![]() m+2)、M(m,
m+2)、M(m,![]() m﹣2),
m﹣2),
则QM=﹣![]() m2+
m2+![]() m+2﹣(
m+2﹣(![]() m﹣2)=﹣
m﹣2)=﹣![]() m2+m+4,
m2+m+4,
∵F(0,![]() )、D(0,﹣2),
)、D(0,﹣2),
∴DF=![]() ,
,
∵QM∥DF,
∴当|﹣![]() m2+m+4|=
m2+m+4|=![]() 时,四边形DMQF是平行四边形,
时,四边形DMQF是平行四边形,
解得:m=﹣1或m=3或m=1+![]() 或1﹣
或1﹣![]()
即m=﹣1或m=3或m=1+![]() 或1﹣
或1﹣![]() 时,四边形DMQF是平行四边形.
时,四边形DMQF是平行四边形.

 小学教材全测系列答案
小学教材全测系列答案