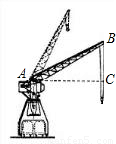
题目内容
如图,一起重机的机身高21米,吊杆AB长36米,吊杆与水平线的夹角∠BAC可从![]() 升到
升到![]() .求起重机起吊的最大高度(吊钩本身的长度和所挂重物的高度忽略不计)和当起重机位置不变时可使用的最大水平距离(精确到0.1米,
.求起重机起吊的最大高度(吊钩本身的长度和所挂重物的高度忽略不计)和当起重机位置不变时可使用的最大水平距离(精确到0.1米,![]() =0.9848,
=0.9848,![]() =0.1736,
=0.1736,![]() ≈1.732).
≈1.732).

答案:
解析:
提示:
解析:
|
解:在Rt△ABC中,当∠BAC= BC=AB· =36×0.9848≈35.5(米). 35.5+21=56.5(米). 当∠BAC= AC=AB· ≈18×1.732≈31.2(米). 答:最大高度约为56.5米,最大水平距离约31.2米. |
提示:
|
这是一个解直角三角形的应用问题.当已知直角三角形的边与角时,可利用三角函数,求未知的边. |

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
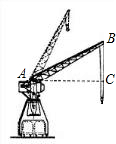 如图,一起重机的机身高21m,吊杆AB长36m,吊杆与水平线的夹角∠BAC可从30°升到80°.求起重机起吊的最大高度(吊钩本身的长度和所挂重物的高度忽略不计)和当起重机位置不变时使用的最大水平距离(精确到0.1米,sin80°=0.9848,cos80°=0.1736,
如图,一起重机的机身高21m,吊杆AB长36m,吊杆与水平线的夹角∠BAC可从30°升到80°.求起重机起吊的最大高度(吊钩本身的长度和所挂重物的高度忽略不计)和当起重机位置不变时使用的最大水平距离(精确到0.1米,sin80°=0.9848,cos80°=0.1736,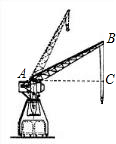 如图,一起重机的机身高21m,吊杆AB长36m,吊杆与水平线的夹角∠BAC可从30°升到80°.求起重机起吊的最大高度(吊钩本身的长度和所挂重物的高度忽略不计)和当起重机位置不变时使用的最大水平距离(精确到0.1米,sin80°=0.9848,cos80°=0.1736,
如图,一起重机的机身高21m,吊杆AB长36m,吊杆与水平线的夹角∠BAC可从30°升到80°.求起重机起吊的最大高度(吊钩本身的长度和所挂重物的高度忽略不计)和当起重机位置不变时使用的最大水平距离(精确到0.1米,sin80°=0.9848,cos80°=0.1736, ≈1.732)
≈1.732) ≈1.732)
≈1.732)
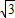 ≈1.732)
≈1.732)