题目内容
 如图,在⊙O中,直径AB与弦CD相交于点E,∠BED=60°,AE=2,BE=6,则CD的长为________.
如图,在⊙O中,直径AB与弦CD相交于点E,∠BED=60°,AE=2,BE=6,则CD的长为________.
2
分析:作OM⊥CD于点M,连接OC,在直角三角形OEM中,根据三角函数求得OM的长,然后在直角△OCM中,利用勾股定理即可求得CM的长,进而求得CD的长.
解答: 作OM⊥CD于点M,连接OC.
作OM⊥CD于点M,连接OC.
OC=OA=OB= (AE+BE)=4
(AE+BE)=4
∴OE=OA-AE=4-2=2.
在Rt△OME中,sin∠OED=
∴OM=OE•sin∠OED=2× =
= .
.
在Rt△OCM中,CM= =
= =
= .
.
∴CD=2CM=2 .
.
点评:本题考查了垂径定理,以及勾股定理,正确求得OM的长是关键.

分析:作OM⊥CD于点M,连接OC,在直角三角形OEM中,根据三角函数求得OM的长,然后在直角△OCM中,利用勾股定理即可求得CM的长,进而求得CD的长.
解答:
 作OM⊥CD于点M,连接OC.
作OM⊥CD于点M,连接OC.OC=OA=OB=
 (AE+BE)=4
(AE+BE)=4∴OE=OA-AE=4-2=2.
在Rt△OME中,sin∠OED=

∴OM=OE•sin∠OED=2×
 =
= .
.在Rt△OCM中,CM=
 =
= =
= .
.∴CD=2CM=2
 .
.点评:本题考查了垂径定理,以及勾股定理,正确求得OM的长是关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
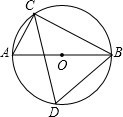 如图,在⊙O中,直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,则BC=
如图,在⊙O中,直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,则BC=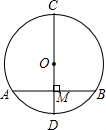 如图,在⊙O中,直径CD的长度为10cm,AB是弦,且AB⊥CD于M,OM=3cm,求弦AB的长.
如图,在⊙O中,直径CD的长度为10cm,AB是弦,且AB⊥CD于M,OM=3cm,求弦AB的长.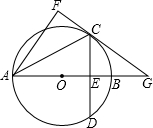 C与直线AB相交于点G.
C与直线AB相交于点G. (2013•百色)如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠ABO的度数是( )
(2013•百色)如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠ABO的度数是( ) (2012•朝阳区二模)如图,在⊙O中,直径AB⊥弦CD于点H,E是⊙O上的点,若∠BEC=25°,则∠BAD的度数为( )
(2012•朝阳区二模)如图,在⊙O中,直径AB⊥弦CD于点H,E是⊙O上的点,若∠BEC=25°,则∠BAD的度数为( )