Question

【题目】如图，在平面直角坐标系中，矩形的两边、分别在轴、轴的正半轴上，反比例函数（＞0）与相交于点，与相交于点，若，且的面积是5，则的值为_______．

Answer 1

【答案】

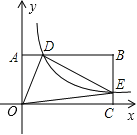
【解析】试题分析：设B点的坐标为（a，b），根据矩形的性质以及BE=4EC，表示出E、D两点的坐标，根据S△ODE=S矩形OCBA﹣S△AOD﹣S△OCE﹣S△BDE=5，求出B的横纵坐标的积，进而求出反比例函数的比例系数．

解：∵四边形OCBA是矩形，

∴AB=OC，OA=BC，

设B点的坐标为（a，b），

∵BE=4EC，

∴E（a，b），

∵点D，E在反比例函数的图象上，

∴ab=k，∴D（a，b），

∵S△ODE=S矩形OCBA﹣S△AOD﹣S△OCE﹣S△BDE

=ab﹣

ab﹣

ab﹣（a﹣a）（b﹣b）

=ab=5，

∴ab=，

∴k=ab=．

故答案为．