题目内容
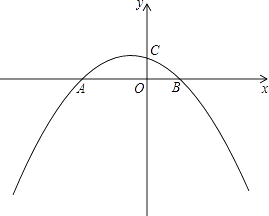
【题目】抛物线y=ax2+bx+3经过点A（1，0）和点B（5，0）．
（1）求该抛物线所对应的函数解析式；
（2）该抛物线与直线y= 
x+3相交于C、D两点，点P是抛物线上的动点且位于x轴下方，直线PM∥y轴，分别与x轴和直线CD交于点M、N．
①连结PC、PD，如图1，在点P运动过程中，△PCD的面积是否存在最大值？若存在，求出这个最大值；若不存在，说明理由；
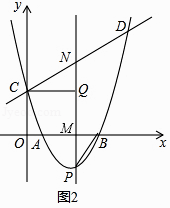
②连结PB，过点C作CQ⊥PM，垂足为点Q，如图2，是否存在点P，使得△CNQ与△PBM相似？若存在，求出满足条件的点P的坐标；若不存在，说明理由．
【答案】
（1）
解：∵抛物线y=ax2+bx+3经过点A（1，0）和点B（5，0），
∴ 
，解得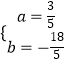 
，
∴该抛物线对应的函数解析式为y= 
x2﹣ 
x+3
（2）
解：①∵点P是抛物线上的动点且位于x轴下方，
∴可设P（t， t2﹣ t+3）（1＜t＜5），
∵直线PM∥y轴，分别与x轴和直线CD交于点M、N，
∴M（t，0），N（t， t+3），
∴PN= t+3﹣（ t2﹣ t+3）=﹣ （t﹣ 
）2+ 
联立直线CD与抛物线解析式可得 
，解得 
或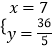 
，
∴C（0，3），D（7， 
），
分别过C、D作直线PN的直线，垂足分别为E、F，如图1，
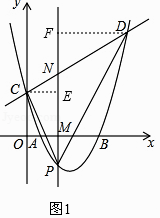
则CE=t，DF=7﹣t，
∴S△PCD=S△PCN+S△PDN= 
PNCE+ PNDF= PN= [﹣ （t﹣ ）2+ ]=﹣ 
（t﹣ ）2+ 
，
∴当t= 时，△PCD的面积有最大值，最大值为
②存在．
∵∠CQN=∠PMB=90°，
∴当△CNQ与△PBM相似时，有 
= 
或 
= 
两种情况，
∵CQ⊥PM，垂足为Q，
∴Q（t，3），且C（0，3），N（t， t+3），
∴CQ=t，NQ= t+3﹣3= t，
∴ 
= ，
∵P（t， t2﹣ t+3），M（t，0），B（5，0），
∴BM=5﹣t，PM=0﹣（ t2﹣ t+3）=﹣ t2+ t﹣3，
当 = 时，则PM= BM，即﹣ t2+ t﹣3= （5﹣t），解得t=2或t=5（舍去），此时P（2， 
）；
当 = 时，则BM= PM，即5﹣t= （﹣ t2+ t﹣3），解得t= 
或t=5（舍去），此时P（ ，﹣ 
）；
综上可知存在满足条件的点P，其坐标为（2， ）或（ ，﹣ ）
【解析】（1）由A、B两点的坐标，利用待定系数法可求得抛物线解析式；（2）①可设出P点坐标，则可表示出M、N的坐标，联立直线与抛物线解析式可求得C、D的坐标，过C、D作PN的垂线，可用t表示出△PCD的面积，利用二次函数的性质可求得其最大值；②当△CNQ与△PBM相似时有 = 或 = 两种情况，利用P点坐标，可分别表示出线段的长，可得到关于P点坐标的方程，可求得P点坐标．
【考点精析】利用相似三角形的判定与性质对题目进行判断即可得到答案，需要熟知相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．
