题目内容
等边△ABC中,D、E分别为AC、AB上的点,且AD=BE,BD、CE交于点P,过点C作CQ⊥BD于点Q,若PE=1,PQ=3,则BD=
7
7
.分析:首先延长PQ,使得QF=PQ,连接CF,易得CF=CP,易证得△ABD≌△BCE,继而证得△PCF是等边三角形,则可求得答案.
解答: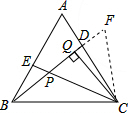 解:延长PQ,使得QF=PQ,连接CF,
解:延长PQ,使得QF=PQ,连接CF,
∵CQ⊥BD,
∴CF=CP,
∵△ABC是等边三角形,
∴AB=BC,∠A=∠ABC=60°,
在△ABD和△BCE中,
,
∴△ABD≌△BCE(SAS),
∴BD=CE,∠ABD=∠BCE,
∴∠CPD=∠PBC+∠BCE=∠PBC+∠ABD=∠ABC=60°,
∴△PCF是等边三角形,
∴PC=PF=2PQ=6,
∴BD=CE=PC+PE=6+1=7.
故答案为:7.
 解:延长PQ,使得QF=PQ,连接CF,
解:延长PQ,使得QF=PQ,连接CF,∵CQ⊥BD,
∴CF=CP,
∵△ABC是等边三角形,
∴AB=BC,∠A=∠ABC=60°,
在△ABD和△BCE中,
|
∴△ABD≌△BCE(SAS),
∴BD=CE,∠ABD=∠BCE,
∴∠CPD=∠PBC+∠BCE=∠PBC+∠ABD=∠ABC=60°,
∴△PCF是等边三角形,
∴PC=PF=2PQ=6,
∴BD=CE=PC+PE=6+1=7.
故答案为:7.
点评:此题考查了等边三角形的判定与性质以及全等三角形的判定与性质.此题难度较大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
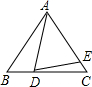 如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的边长为( )
如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的边长为( )| A、9 | B、12 | C、15 | D、18 |
 如图,边长为4的等边△ABC中,DE为中位线,则四边形BCED的面积为( )
如图,边长为4的等边△ABC中,DE为中位线,则四边形BCED的面积为( )A、2
| ||
B、3
| ||
C、4
| ||
D、6
|
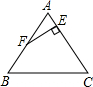 如图,等边△ABC中,F是AB中点,EF⊥AC于E,若△ABC的边长为10,则AE=
如图,等边△ABC中,F是AB中点,EF⊥AC于E,若△ABC的边长为10,则AE= 7、如图,在等边△ABC中,取BD=CE=AF,且D,E,F非所在边中点,由图中找出3个全等三角形组成一组,这样的全等三角形的组数有( )
7、如图,在等边△ABC中,取BD=CE=AF,且D,E,F非所在边中点,由图中找出3个全等三角形组成一组,这样的全等三角形的组数有( ) 如图,等边△ABC中,D、E分别为AC、AB上两点,下列结论:
如图,等边△ABC中,D、E分别为AC、AB上两点,下列结论: