题目内容
 如图,已知AD∥BC,AP平分∠DAB,BP平分∠ABC,点P恰好在CD上,则PD与PC的大小关系是
如图,已知AD∥BC,AP平分∠DAB,BP平分∠ABC,点P恰好在CD上,则PD与PC的大小关系是
- A.PD>PC
- B.PD=PC
- C.PD<PC
- D.无法判断
B
分析:作PE∥AB与E点,利用角平分线的性质可以得到PA=PE,PB=PE,从而得到结论.
解答: 解:作PE∥AD,交AB于点E.
解:作PE∥AD,交AB于点E.
∵AD∥BC,
∴PE∥BC
∴∠DAP=∠EPA
∵AP平分∠DAB,
∴∠DAP=∠BAP,
∴∠EAP=∠EPA,
∴AE=EP,
同理可证EP=EB,
∴E为BA的中点,
∴P为DC的中点,
∴PD=PC,
故选B.
点评:本题考查了梯形的中位线的性质,解题的关键是正确地作出辅助线.
分析:作PE∥AB与E点,利用角平分线的性质可以得到PA=PE,PB=PE,从而得到结论.
解答:
 解:作PE∥AD,交AB于点E.
解:作PE∥AD,交AB于点E.∵AD∥BC,
∴PE∥BC
∴∠DAP=∠EPA
∵AP平分∠DAB,
∴∠DAP=∠BAP,
∴∠EAP=∠EPA,
∴AE=EP,
同理可证EP=EB,
∴E为BA的中点,
∴P为DC的中点,
∴PD=PC,
故选B.
点评:本题考查了梯形的中位线的性质,解题的关键是正确地作出辅助线.

练习册系列答案
相关题目
 9、如图,已知AD∥BC,∠1=∠2,∠A=112°,且BD⊥CD,则∠ABC=
9、如图,已知AD∥BC,∠1=∠2,∠A=112°,且BD⊥CD,则∠ABC= 如图,已知AD=BC.EC⊥AB.DF⊥AB,C.D为垂足,要使△AFD≌△BEC,还需添加一个条件.若以“ASA”为依据,则添加的条件是
如图,已知AD=BC.EC⊥AB.DF⊥AB,C.D为垂足,要使△AFD≌△BEC,还需添加一个条件.若以“ASA”为依据,则添加的条件是 如图,已知AD=BC,AC=BD,∠DAC与∠CBD有什么关系?说说你的理由.
如图,已知AD=BC,AC=BD,∠DAC与∠CBD有什么关系?说说你的理由.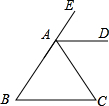 如图,已知AD∥BC,AD平分∠CAE,试说明△ABC是等腰三角形.
如图,已知AD∥BC,AD平分∠CAE,试说明△ABC是等腰三角形. 如图,已知AD∥BC,∠1=∠2,∠A=112°,且BD⊥CD,则∠C=
如图,已知AD∥BC,∠1=∠2,∠A=112°,且BD⊥CD,则∠C=