题目内容
一次函数y=4（x+6）与坐标轴围成的三角形的面积是________．
72
分析：图象与坐标轴围成的三角形是直角三角形，只要求出两直角边长，即可求面积，而直角边长需要计算一次函数图象与坐标轴的交点坐标．
解答：令x=0，得y=24，令y=0，得x=-6；
所以，图象与坐标轴围成的三角形面积为：24×6÷2=72．
故填72．
点评：本题考查了一次函数图象上的两个特殊点（与坐标轴的交点）在计算三角形面积中的作用．
分析：图象与坐标轴围成的三角形是直角三角形，只要求出两直角边长，即可求面积，而直角边长需要计算一次函数图象与坐标轴的交点坐标．
解答：令x=0，得y=24，令y=0，得x=-6；
所以，图象与坐标轴围成的三角形面积为：24×6÷2=72．
故填72．
点评：本题考查了一次函数图象上的两个特殊点（与坐标轴的交点）在计算三角形面积中的作用．
练习册系列答案
阅读快车系列答案
相关题目
为保护学生视力，课桌椅的高度都是按一定的关系配套设计的，研究表明：假设课桌的高度为ycm，椅子的高度为xcm，则y应是x的一次函数，下表列出两套符合条件的课桌椅的高度：第一套第二套椅子高度xcm桌子高度ycm．
（1）请确定y与x的函数关系式．
（2）现有一把高39cm的椅子和一张高为78.2的课桌，它们是否配套？为什么？
| 第一套 | 第二套 | |
| 椅子高度xcm | 40 | 37 |
| 桌子高度ycm | 75 | 70 |
（2）现有一把高39cm的椅子和一张高为78.2的课桌，它们是否配套？为什么？
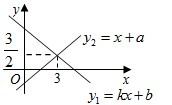一次函数y1=kx+b与y2=x+a的图象如图，下列结论中：