Question

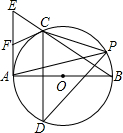
已知：D为⊙O上一点，C为

AB

的中点，弦AB、CD相交于点H，延长AB到点E，使ED=EH．
（1）求证：直线ED与⊙O相切；
（2）若⊙O半径为2，

AB

=π，求弦AB的长．

Answer 1

分析：（1）连接OD，OC，OC交AB于F，根据垂径定理得出OC⊥AB，求出∠C+∠FHC=90°，根据∠DHE=∠CHF，∠EDH=∠DHE，∠C=∠ODC，推出∠ODC+∠EDH=90°，得出OD⊥DE，根据切线的判定推出即可；
（2）根据弧长公式求出∠AOB，求出∠AOC，根据解直角三角形求出AH，即可求出答案．

解答：（1）证明：连接OD，OC，OC交AB于F，
∵C为弧AB中点，OC为半径，
∴OC⊥AB，
∴∠CFH=90°，
∴∠C+∠FHC=90°，
∵∠DHE=∠CHF，
∴∠C+∠DHE=90°，
∵DE=EH，OD=OC，
∴∠EDH=∠DHE，∠C=∠ODC，
∴∠ODC+∠EDH=90°，
∴OD⊥DE，
∵OD为半径，
∴直线ED与⊙O相切；

（2）解：连接OA、OB，
∵⊙O半径为2，弧AB=π，设∠AOB=n°，
∴

nπ×2

180

=π，
n=90，
∴∠AOB=90°，
∵OA=OB，OC⊥AB，
∴∠AOC=45°，AB=2AF，
∴cos45°=

AF

OA

∵OA=2，
∴AF=

2

，
AB=2AF=2

2

．

点评：本题考查了切线的判定，等腰三角形的性质，对顶角相等，弧长公式，解直角三角形等知识点的综合运用．