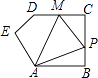题目内容
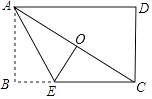
【题目】如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分的面积为( ) 
A.![]()
B.![]()
C.1﹣ ![]()
D.1﹣ ![]()
【答案】C
【解析】解:如图,设B′C′与CD的交点为E,连接AE, 在Rt△AB′E和Rt△ADE中, ![]() ,
,
∴Rt△AB′E≌Rt△ADE(HL),
∴∠DAE=∠B′AE,
∵旋转角为30°,
∴∠DAB′=60°,
∴∠DAE= ![]() ×60°=30°,
×60°=30°,
∴DE=1× ![]() =
= ![]() ,
,
∴阴影部分的面积=1×1﹣2×( ![]() ×1×
×1× ![]() )=1﹣
)=1﹣ ![]() .
.
故选:C.
设B′C′与CD的交点为E,连接AE,利用“HL”证明Rt△AB′E和Rt△ADE全等,根据全等三角形对应角相等∠DAE=∠B′AE,再根据旋转角求出∠DAB′=60°,然后求出∠DAE=30°,再解直角三角形求出DE,然后根据阴影部分的面积=正方形ABCD的面积﹣四边形ADEB′的面积,列式计算即可得解.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目