题目内容
 如图,点D、E、F分别在正三角形ABC的三边上,且△DEF也是正三角形,若△ABC的边长为a,△DEF的边长为b.则△AEF的内切圆半径为________.
如图,点D、E、F分别在正三角形ABC的三边上,且△DEF也是正三角形,若△ABC的边长为a,△DEF的边长为b.则△AEF的内切圆半径为________.
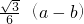
分析:欲求△AEF的内切圆半径,可以画出图形,然后利用题中已知条件,挖掘隐含条件求解.
解答:
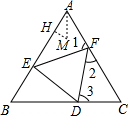 解:如图,由于△ABC,△DEF都为正三角形,
解:如图,由于△ABC,△DEF都为正三角形,∴AB=BC=CA,EF=FD=DE,∠BAC=∠B=∠C=∠FED=∠EFD=∠EDF=60°,
∴∠1+∠2=∠2+∠3=120°,∠1=∠3;
在△AEF和△CFD中,
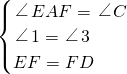 ,
,∴△AEF≌△CFD(AAS);
同理可证:△AEF≌△CFD≌△BDE;
∴BE=AF,即AE+AF=AE+BE=a.
设M是△AEF的内心,MH⊥AE于H,
则AH=
 (AE+AF-EF)=
(AE+AF-EF)= (a-b);
(a-b);∵MA平分∠BAC,
∴∠HAM=30°;
∴HM=AH•tan30°=
 (a-b)•
(a-b)• =
= (a-b).
(a-b).故答案为:
 (a-b).
(a-b).点评:本题考查了等边三角形的性质以及全等三角形的判定与性质以及内心的性质,根据已知得出AH的长是解题关键.

练习册系列答案
相关题目
 如图,点D,E,F分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( )
如图,点D,E,F分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( )| A、EF与AD互相平分 | ||
B、EF=
| ||
| C、AD平分∠BAC | ||
| D、△DEF∽△ACB |
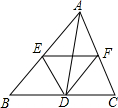 如图,点D,E,F分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( )
如图,点D,E,F分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( )| A、AD平分∠BAC | ||
B、EF=
| ||
| C、EF与AD互相平分 | ||
| D、△DFE是△ABC的位似图形 |
 5、如图,点D、E、F分别是△ABC的边AB、BC、AC的中点,连接DE、EF,要使四边形ADEF为正方形,还需增加条件:
5、如图,点D、E、F分别是△ABC的边AB、BC、AC的中点,连接DE、EF,要使四边形ADEF为正方形,还需增加条件: 如图,点D,E,F分别是△ABC的三边AB,AC,BC上的中点,如果△ABC的面积是18cm2,则△DBF的面积是
如图,点D,E,F分别是△ABC的三边AB,AC,BC上的中点,如果△ABC的面积是18cm2,则△DBF的面积是 如图,点D、E、F分别是△ABC三边AB、BC、AC的中点,则△DEF的周长是△ABC周长的( )
如图,点D、E、F分别是△ABC三边AB、BC、AC的中点,则△DEF的周长是△ABC周长的( )