��Ŀ����
����Ŀ����ͼ��������![]() ���ʾ��
���ʾ��![]() ��
��![]() ���ʾ��
���ʾ��![]() ����
����![]() ��
��![]() ����
����![]()
![]()
![]() ��
��![]() ��ʾ����Ϊ________����
��ʾ����Ϊ________����![]() ��ʾ����Ϊ________��
��ʾ����Ϊ________��
![]() ����
����![]() ���
���![]() ֮��ľ����ʾΪ
֮��ľ����ʾΪ![]() ����
����![]() ���
���![]() ֮��ľ����ʾΪ
֮��ľ����ʾΪ![]() ��������������һ��
��������������һ��![]() ��ʹ
��ʹ![]() ����
����![]() ���ʾ����________��
���ʾ����________��
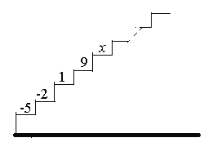
![]() ����ԭ��
����ԭ��![]() ����һ���壬һС��״ӵ�
����һ���壬һС��״ӵ�![]() ����
����![]() ����λ/����ٶ������˶���ͬʱ��һС���Ҵӵ�
����λ/����ٶ������˶���ͬʱ��һС���Ҵӵ�![]() ����
����![]() ����λ/����ٶ�Ҳ�����˶������������������Ĵ�С���ɿ���һ�㣩��ԭ�����ٶ����෴�ķ����˶������˶���ʱ��Ϊ
����λ/����ٶ�Ҳ�����˶������������������Ĵ�С���ɿ���һ�㣩��ԭ�����ٶ����෴�ķ����˶������˶���ʱ��Ϊ![]() ���룩����ֱ��ʾ���ס�����С��ԭ��ľ��루�ú�
���룩����ֱ��ʾ���ס�����С��ԭ��ľ��루�ú�![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
���𰸡���1��-5��7����2��4��13����3����0��t��3.5ʱ��С��ԭ��ľ���Ϊ7��2t����t��3.5ʱС��ԭ��ľ���Ϊ2t��7��
��������
��1�����ݷǸ����������з������a��b��ֵ���Ӷ��ý⣻
��2��������������ı�ʾ�г�����ֵ���̣�Ȼ����⼴�ɣ�
��3����С����������ϵ����������ʾ���ɣ���С��������������ƶ��������ֱַ���ʽ��ʾ���ɣ�
��1��������ã�a+5=0��b��7=0��
���a=��5��b=7��
���ԣ���A��ʾ��5����B��ʾ7��
��2�����C��ʾx��������ã�|��5��x|=3|7��x|��
���ԣ�5+x=3��7��x����5+x=��3��7��x����
���x=4����x=13��
���ԣ���C��ʾ����Ϊ4��13��
��3���ף���С��״ӵ�A����1����λ/����ٶ������˶���
���ԭ��ľ���Ϊ|��5��t|=5+t��
��С���Ҵӵ�B����2����λ/����ٶ�Ҳ�����˶���
���ҵ���ԭ���ʱ��Ϊ7��2=3.5��
�൱0��t��3.5ʱ��С��ԭ��ľ���Ϊ7��2t��
��t��3.5ʱС��ԭ��ľ���Ϊ2t��7��

����Ŀ����������Ϫˮ��ľ���ˮλ��![]() ����������Ϫˮ����������·�ij�ܼ���ˮλ�仯���������ĩǡ�ôﵽ����ˮλ��������ʾ��ǰһ��ˮλ�ߣ�������ʾ��ǰһ��ˮλ�ͣ���
����������Ϫˮ����������·�ij�ܼ���ˮλ�仯���������ĩǡ�ôﵽ����ˮλ��������ʾ��ǰһ��ˮλ�ߣ�������ʾ��ǰһ��ˮλ�ͣ���
���� | һ | �� | �� | �� | �� | �� | �� |
ˮλ�仯 |
|
|
|
|
|
|
|

![]() �����ĵ�ˮλ�Ƕ��٣�
�����ĵ�ˮλ�Ƕ��٣�
![]() ������һ�����������ˮλ����ߵģ�
������һ�����������ˮλ����ߵģ�
![]() �Ծ���ˮλΪ��㣬������ͼ����ʾ����ˮλ�����
�Ծ���ˮλΪ��㣬������ͼ����ʾ����ˮλ�����