题目内容
如图，若∠1+∠2=180°，∠3=110°，则∠4的度数等于
- A.∠1
- B.110°
- C.180°-∠2
- D.70°
D
分析：根据已知条件和平角的定义求得同位角∠1=∠5，从而推知两直线a∥b；然后由平行线的性质及对顶角相等来求∠4的度数．
解答：
解：∵∠1+∠2=180°（已知），
∠2+∠5=180°（平角是180°），
∴∠1=∠5（等量代换），
∴a∥b（同位角相等，两直线平行）；
∴∠4+∠6=180°（两直线平行，同旁内角互补）；
又∵∠3=∠6（对顶角相等），∠3=110°，
∴∠4=70°．
故选D．
点评：本题考查了平行线的判定与性质．解答此题的关键是注意平行线的性质和判定定理的综合运用．
分析：根据已知条件和平角的定义求得同位角∠1=∠5，从而推知两直线a∥b；然后由平行线的性质及对顶角相等来求∠4的度数．
解答：
解：∵∠1+∠2=180°（已知），∠2+∠5=180°（平角是180°），
∴∠1=∠5（等量代换），
∴a∥b（同位角相等，两直线平行）；
∴∠4+∠6=180°（两直线平行，同旁内角互补）；
又∵∠3=∠6（对顶角相等），∠3=110°，
∴∠4=70°．
故选D．
点评：本题考查了平行线的判定与性质．解答此题的关键是注意平行线的性质和判定定理的综合运用．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
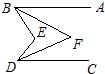如图，若AB∥CD，∠ABE和∠CDE的平分线交于点F，且∠BED=75°，那么∠BFD等于（ ）| A、35° | B、37.5° | C、38.5° | D、36° |
如图，若大圆半径为R，小圆面积是大圆面积的
（1997•重庆）如图．若△ABC的BC边上的高为AH，BC长为30cm，DE∥BC，以DE为直径的半圆与BC切于F，若此半圆的面积是18πcm2，则AH=