题目内容
平行四边形 中,
中, ,
, ,
, 为
为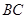 边上的高,将
边上的高,将 沿
沿 所在直线翻折后得
所在直线翻折后得 ,那么
,那么 与四边形
与四边形 重叠部分的面积是
重叠部分的面积是

解析试题分析:先根据题意画出图形,由折叠的性质可得 ≌
≌ ,则可得∠F=∠B=60°,设CD与AF相交于点P,根据平行四边形的性质推出△CFP为等边三角形,再根据
,则可得∠F=∠B=60°,设CD与AF相交于点P,根据平行四边形的性质推出△CFP为等边三角形,再根据 与四边形AECD重叠部分的面积是△AEF与△CFP的面积之差即可求得结果.
与四边形AECD重叠部分的面积是△AEF与△CFP的面积之差即可求得结果.
由题意得 ≌
≌
∴∠F=∠B=60°,
在△ABE中,∠B=60°,AB=8,
则 ,BE=4
,BE=4
∴ ,CF=EF-EC=BE-(BC-BE)=2
,CF=EF-EC=BE-(BC-BE)=2
∵在平行四边形ABCD中,CD∥AB
∴∠PCF=∠B=60°=∠F,
∴△CFP为等边三角形,底边2,高为
∴
∴

考点:折叠的性质,全等三角形的判定和性质,平行四边形的性质
点评:解答本题的关键是熟练掌握折叠的性质:折叠前后图形的对应边、对应角相等.

练习册系列答案
相关题目
 将完全相同的平行四边形和完全相同的菱形镶嵌成如图所示的图案.设菱形中较小角为x度,平行四边形中较大角为y度,则y与x的关系式是
将完全相同的平行四边形和完全相同的菱形镶嵌成如图所示的图案.设菱形中较小角为x度,平行四边形中较大角为y度,则y与x的关系式是 中,以点
中,以点 为圆心,
为圆心, 为半径的圆,交
为半径的圆,交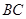 于点
于点 .
.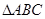 ≌
≌ ;
; ,
, ,
, ,求
,求 的长.
的长.