题目内容
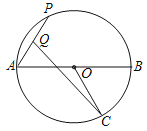
【题目】在![]() 中,
中,![]() ,点
,点![]() 分别是边
分别是边![]() 、
、![]() 的中点,将
的中点,将![]() 绕着点
绕着点![]() 旋转,点
旋转,点![]() 旋转后的对应点分别为点
旋转后的对应点分别为点![]() ,当直线
,当直线![]() 经过点
经过点![]() 时,线段
时,线段![]() 的长为____________
的长为____________
【答案】![]() 或
或![]()
【解析】
当直线![]() 经过点
经过点![]() 时,有两种情况,均用三点共线特征及勾股定理求出AE长为5或3,采用两边对应成比例且夹角相等证得△CBD∽△ABE,利用相似三角形对应边成比例求解.
时,有两种情况,均用三点共线特征及勾股定理求出AE长为5或3,采用两边对应成比例且夹角相等证得△CBD∽△ABE,利用相似三角形对应边成比例求解.
解:在Rt△ACB中,![]() ,
,
由勾股定理得,AB=![]() ,
,
∵![]() 分别是边
分别是边![]() 、
、![]() 的中点,
的中点,
∴DE是△ACB的中位线,BD=2,BE=![]() ,
,
∴DE∥AC,DE=![]()
∴∠EDB=90°,
由旋转可得,BD=2,DE=1,BE=![]() ,∠BDE=90°,
,∠BDE=90°,
第一种情况,如图1,
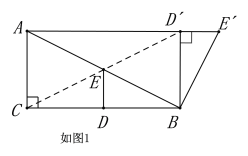
∵点A,D,E三点共线,
∴∠ADB=90°,
由勾股定理得AD=![]() ,
,
∴AE=AD+DE=5
∵∠ABC=∠DBE,
∴∠CBD=∠ABE,
∵![]() ,
,
∴△CBD∽△ABE,
∴![]() ,
,
∴![]() ,
,
∴CD=![]()
第一种情况,如图2,
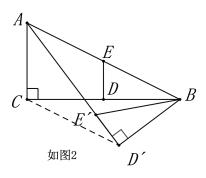
∵点A,D,E三点共线,
∴∠ADB=90°,
由勾股定理得AD=![]() ,
,
∴AE=AD-DE=3
∵∠ABC=∠DBE,
∴∠CBD=∠ABE,
∵![]() ,
,
∴△CBD∽△ABE,
∴![]() ,
,
∴![]() ,
,
∴CD=![]()
∴CD长为![]() 或
或![]() .
.
故答案为:![]() 或
或![]() .
.

练习册系列答案
相关题目