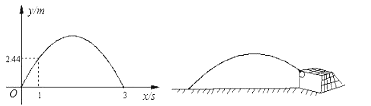
题目内容
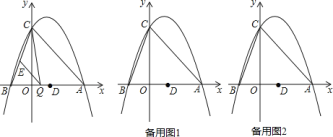
如图,抛物线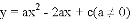 与
与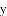
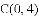
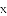
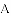
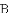
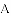
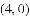
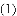
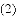
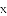
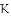
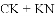
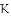
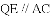
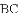
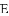
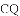
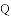
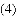
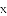

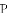
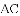
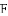
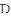
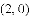

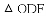
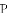
练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目




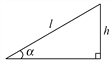
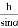 B.
B. 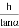 C.
C. 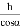 D. h·sinα
D. h·sinα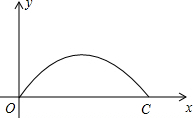
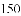
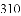
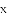
 x2-4x+5化为y=a(x+m)2+k的形式,再指出该函数图象的开口方向、对称轴和顶点坐标.
x2-4x+5化为y=a(x+m)2+k的形式,再指出该函数图象的开口方向、对称轴和顶点坐标.