题目内容
已知:如图四,在平面直角坐标系中,点O为坐标原点,以y轴负半轴上一点A为圆心,5为半径作圆A,交x轴于点B、点C,交y轴于点D、点E,tan∠DBO=![]() .
.
求:(1)点D的坐标;
(2)直线CD的函数解析式.
 |
解:(1)∵在Rt△BDO中,tan∠DBO=![]()
∴![]() =
=![]() ,设DO=a,则BO=2a…………………………………………………1分
,设DO=a,则BO=2a…………………………………………………1分
联结AB,∵圆A的半径为5,∴AB=AD=5,AO=5-a …………………………1分
∵在Rt△ABO中,AO2+BO2=AB2,∴(5-a)2+(2a)2=52 …………………1分
∴a1=2,a2=0(舍) …………………………………………………………………1分
∴D(0,2) ……………………………………………………………………………1分
(2)∵AD⊥BC,∴BO=CO=2a=4 …………………………………………………1分
∴C(4,0) ……………………………………………………………………………1分
设直线CD的函数解析式为y=kx+b(k≠0),把C(4,0),D(0,2)代入,
得![]() ,∴
,∴ …………………………………………………………2分
…………………………………………………………2分
∴直线CD的函数解析式为y=-![]() x+2 ……………………………………………1分
x+2 ……………………………………………1分

练习册系列答案
相关题目

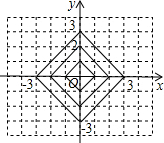 已知:如图,在平面直角坐标系xOy中,横、纵坐标都为整数的点称为整点.观察图中每一个正方形(实践)四条边上的整点的个数.
已知:如图,在平面直角坐标系xOy中,横、纵坐标都为整数的点称为整点.观察图中每一个正方形(实践)四条边上的整点的个数. 相交于点C.
相交于点C.