题目内容
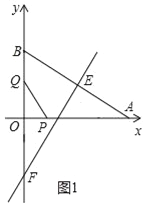
【题目】如图,在Rt△AOB中,∠AOB=90°,AO=![]() ,BO=1,AB的垂直平分线交AB于点E,交射线BO于点F,点P从点A出发沿射线AO以每秒2
,BO=1,AB的垂直平分线交AB于点E,交射线BO于点F,点P从点A出发沿射线AO以每秒2![]() 个单位的速度运动,同时点Q从点O出发沿OB方向以每秒1个单位的速度运动,当点Q到达点B时,点P、Q同时停止运动,设运动的时间为t秒.
个单位的速度运动,同时点Q从点O出发沿OB方向以每秒1个单位的速度运动,当点Q到达点B时,点P、Q同时停止运动,设运动的时间为t秒.
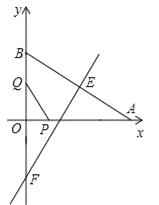
(1)①当t为何值时,PQ∥AB;②当t为何值时,PQ∥EF;
(2)当点P在O的左侧时,记四边形PFEQ的面积为S,求S关于t的函数关系式;
(3)以O为原点,OA所在直线为x轴,建立直角坐标系,若P、Q关于点O的对称点分别为P′、Q′,当线段P′Q′,与线段EF有公共点时,抛物线y=ax2+1经过P′Q′的中点,此时的抛物线与x正半轴交于点M;
①求a的取值范围;
②求点M移动的运动速度.
【答案】(1)①当t=![]() 时,PQ∥AB;②当t=
时,PQ∥AB;②当t=![]() 时,PQ∥E
时,PQ∥E
(2)S=![]() t2+
t2+![]() t﹣
t﹣![]() ;
;
(3)①﹣16≤a≤﹣2
②![]() 单位长度/秒
单位长度/秒
【解析】
试题分析:(1)由△OPQ∽△OAB,得![]() 列出方程即可解决问题.
列出方程即可解决问题.
(2)过点E作EG⊥BF,根据S=![]() QF×EG+
QF×EG+![]() QF×OP=
QF×OP=![]() QF(EG+OP)计算即可.
QF(EG+OP)计算即可.
(3)①由图象3,可知,![]() ≤t≤1时,线段P′Q′,与线段EF有公共点,分别求出t=
≤t≤1时,线段P′Q′,与线段EF有公共点,分别求出t=![]() ,t=1时a的值即可解决问题.
,t=1时a的值即可解决问题.
②分别求出a=﹣16,a=﹣2时,点M坐标即可解决问题.
试题解析:(1)如图1中,①∵PQ∥AB,
∴△OPQ∽△OAB,
∴![]() ,
,
∵AP=2![]() t,OQ=t,OA=
t,OQ=t,OA=![]() ,BO=1,
,BO=1,
∴![]() ,
,
∴t=![]() ,
,
∴当t=![]() 时,PQ∥AB;
时,PQ∥AB;
②∵PQ∥EF,
∴∠QPO=∠ENA,
∵∠AEN=∠QOP=90°,
∴△ANE∽△QOP,
∵∠AOB=90°,
∴tanA=![]() =
=![]() ,
,
∴∠A=∠PQO=30°,
∴![]() =
=![]() ,
,
∴t=![]() ,
,
∴当t=![]() 时,PQ∥EF;
时,PQ∥EF;
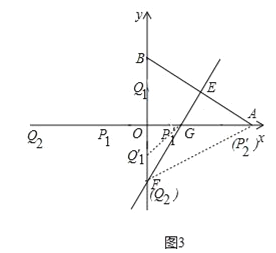
(2)如图2中,过点E作EG⊥BF,
∵∠BAO=30°,
∴∠OBA=90°﹣∠BAO=60°,
∵BG=1﹣t,
∵EF为AB的垂直平分线,
∴BE=1,DF=1,
在Rt△BEA中,∠BEG=60°,BE=1,
∴EG=![]() ,
,
∴S=![]() QF×EG+
QF×EG+![]() QF×OP=
QF×OP=![]() QF(EG+OP)=
QF(EG+OP)=![]() t2+
t2+![]() t﹣
t﹣![]() ;
;
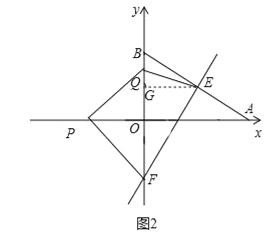
(3)如图3中,①设EF与x轴交于点G.
在RT△AEG中,∵∠AEG=90°,AE=1,∠EAG=30°,
∴cos∠EAG=![]() ,
,
∴AG=![]()
![]() ,OG=
,OG=![]() ,
,
当P′1与点G重合时,t=(![]() +
+![]() )÷2
)÷2![]() =
=![]() ,
,
由图象可知,![]() ≤t≤1时,线段P′Q′,与线段EF有公共点,
≤t≤1时,线段P′Q′,与线段EF有公共点,
当t=![]() 时,P′1Q′1的中点坐标(
时,P′1Q′1的中点坐标(![]() ,﹣
,﹣![]() ),代入y=ax2+1得到,a=﹣16,
),代入y=ax2+1得到,a=﹣16,
当t=1时,P′2Q′2的中点坐标(![]() ,﹣
,﹣![]() ),代入y=ax2+1得到,a=﹣2,
),代入y=ax2+1得到,a=﹣2,
∴﹣16≤a≤﹣2.
②当a=﹣16时,抛物线y=﹣16x2+1,与正半轴交于点M(![]() ,0),
,0),
当a=﹣2时,抛物线y=﹣2x2+1,与正半轴交于点M(![]() ,0),
,0),
∴点M移动的运动速度=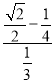 =
=![]() 单位长度/秒.
单位长度/秒.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案