题目内容
在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为 .

【答案】
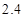
【解析】
试题分析:先求证四边形AFPE是矩形,再根据直线外一点到直线上任一点的距离,垂线段最短,利用相似三角形对应边成比例即可求得AP最短时的长,然后即可求出AM最短时的长.
在△ABC中,AB=6,AC=8,BC=10,
∴∠BAC=90°,
∵PE⊥AB,PF⊥AC,
∴四边形AFPE是矩形,
∴EF=AP.
∵M是EF的中点,
∴AM=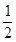 AP,
AP,
根据直线外一点到直线上任一点的距离,垂线段最短,
即AP⊥BC时,AP最短,同样AM也最短,
∴当AP⊥BC时,△ABP∽△CBA,
∴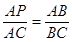 ,
,
∴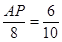 ,
,
∴AP最短时,AP=4.8
∴当AM最短时,AM=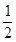 AF=2.4.
AF=2.4.
考点:1.相似三角形判定与性质;2.垂线段最短;3.直角三角形斜边上的中线

练习册系列答案
相关题目




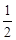 ∠A.
∠A.