题目内容
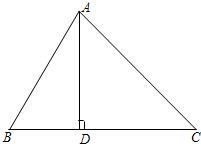已知△ABC中，AD⊥BC于D，已知∠B=60°，∠C=45°，CD=5，试求△ABC的周长（结果保留号）．
解：∵AD⊥BC且∠C=45°
∴△ADC为等腰直角三角形
∴AD=CD=5
∴AC=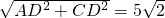
又∵在Rt△ABD中，∠B=60°
∴
；
∴
∴
；
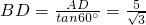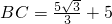
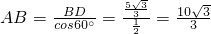∴△ABC的周长=AB+BC+AC
=
=
．
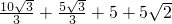
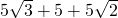分析：将△ABC分成两个Rt△ABD与Rt△ACD，结合三角函数的定义，分别解这两个直角三角形可得其余的边长，进而可得△ABC的周长．
点评：本题考查了解直角三角形的应用，要熟练掌握好边角之间的关系及三角函数的定义．
∴△ADC为等腰直角三角形
∴AD=CD=5
∴AC=
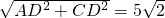
又∵在Rt△ABD中，∠B=60°
∴
；∴
∴
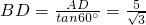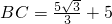
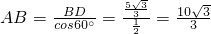；∴△ABC的周长=AB+BC+AC
=
=
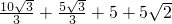
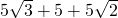．分析：将△ABC分成两个Rt△ABD与Rt△ACD，结合三角函数的定义，分别解这两个直角三角形可得其余的边长，进而可得△ABC的周长．
点评：本题考查了解直角三角形的应用，要熟练掌握好边角之间的关系及三角函数的定义．
练习册系列答案
相关题目
如图，已知△ABC中，AD平分∠BAC交BC于D，AE⊥BC于E，若∠ADE=80°，∠EAC=20°，求∠B的度数．
已知△ABC中，AD⊥BC，E为BC上一点，EG∥AD，分别交AB和CA的延长线于F、G，∠AFG=∠G，
如图，已知△ABC中，AD是BC边上的高，AE是∠BAC的角平分线，若∠C=40°，∠B=64°，求
已知△ABC中，AD平分∠BAC交BC于点D，E是线段AD上一点，EF⊥BC于点F，∠DEF=15°．