题目内容
如图,在四边形ABCD中,AD<BC,对角线AC、BD相交于O点,AC=BD,∠ACB=∠DBC.
(1)求证:四边形ABCD为等腰梯形.
(2)若E为AB上一点,延长DC至F,使CF=BE,连接EF
交BC于G,请判断G点是否为EF中点,并说明理由. (改编)
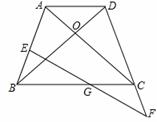
(1)证明:∵∠ACB=∠DBC,∴OB=OC,
 ∵AC=BD,∴OA=OD,∴∠OAD=∠ODA,
∵AC=BD,∴OA=OD,∴∠OAD=∠ODA,
∵∠DOC=∠OAD+∠ODA=∠OBC+∠OCB,
∴2∠OAD=2∠OCB,∴∠OAD=∠OCB,∴AD∥BC
∵AD<BC,∴四边形ABCD为梯形.(2分)
在△ABC和△DCB中:AC=BD,∠ACB=∠DBC,CB=BC.
∴△ABC≌△DCB,∴AB=CD,(2分)∴四边形ABCD为等腰梯形.(1分)
 (2)解:点G是EF中点.(1分)理由:
(2)解:点G是EF中点.(1分)理由:
过E作EH∥CD交BC于H.∴∠EHB=∠DCB,∠EHG=∠GCF,
∵梯形ABCD为等腰梯形,∴∠EBH=∠DCB,
∴∠EBH=∠EHB,∴EB=EH,(2分)
∵EB=CF,∴EH=CF,
在△EHG和△FGC中:∠EHG=∠FCG,∠EGH=∠FGC,EH=CF,
∴△EHG≌△FGC,∴EG=FG即G为EF中点.(2分)

练习册系列答案
相关题目
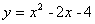 与直线
与直线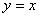 交于点A、B,M是抛物线上一个动点,连接OM。
交于点A、B,M是抛物线上一个动点,连接OM。 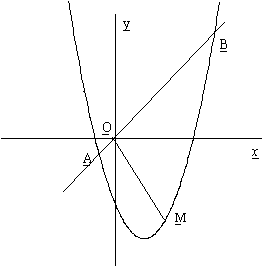
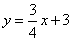 与直线BC:
与直线BC: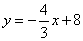 相交于点C,分别交x轴于点A、B,P为x轴上的一点,设P(m,0),以点P为圆心作圆:
相交于点C,分别交x轴于点A、B,P为x轴上的一点,设P(m,0),以点P为圆心作圆:
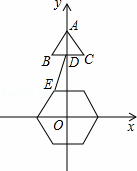

 B.
B.  C.
C.  D.
D.
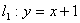 与直线
与直线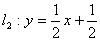 相交于点
相交于点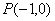 .直线
.直线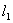 与y轴交于点A.一动点
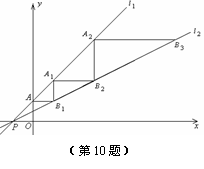
与y轴交于点A.一动点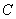 从点A出发,先沿平行于x轴的方向运动,到达直线
从点A出发,先沿平行于x轴的方向运动,到达直线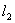 上的点
上的点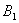 处后,改为垂直于x轴的方向运动,到达直线
处后,改为垂直于x轴的方向运动,到达直线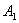 处后,再沿平行于x轴的方向运动,到达直线
处后,再沿平行于x轴的方向运动,到达直线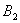 处后,又改为垂直于x轴的方向运动,到达直线
处后,又改为垂直于x轴的方向运动,到达直线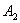 处后,仍沿平行于x轴的方向运动,…… 照此规律运动,动点
处后,仍沿平行于x轴的方向运动,…… 照此规律运动,动点 ,
, ,…,
,…,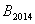 ,
,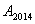 ,…
,… B.
B.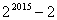 C.
C.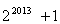 D.
D.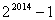
 ,若△DEF的周长为偶数,则 DF的取值为 ( )
,若△DEF的周长为偶数,则 DF的取值为 ( ) 5 (D). 3或4或5
5 (D). 3或4或5 =80,
=80, =80,s
=80,s =240,s
=240,s =180,则成绩较为稳定的班级为 班。
=180,则成绩较为稳定的班级为 班。