题目内容
（2012•岳阳）我们常见的炒菜锅和锅盖都是抛物线面，经过锅心和盖心的纵断面是两端抛物线组合而成的封闭图形，不妨简称为“锅线”，锅口直径为6dm，锅深3dm，锅盖高1dm（锅口直径与锅盖直径视为相同），建立直角坐标系如图①所示，如果把锅纵断面的抛物线记为C1，把锅盖纵断面的抛物线记为C2．
（1）求C1和C2的解析式；
（2）如图②，过点B作直线BE：y=
x-1交C1于点E（-2，-
），连接OE、BC，在x轴上求一点P，使以点P、B、C为顶点的△PBC与△BOE相似，求出P点的坐标；
（3）如果（2）中的直线BE保持不变，抛物线C1或C2上是否存在一点Q，使得△EBQ的面积最大？若存在，求出Q的坐标和△EBQ面积的最大值；若不存在，请说明理由．
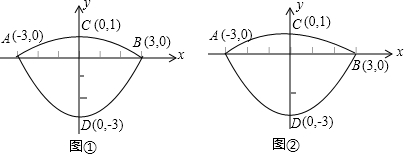
（1）求C1和C2的解析式；
（2）如图②，过点B作直线BE：y=
| 1 |
| 3 |
| 5 |
| 3 |
（3）如果（2）中的直线BE保持不变，抛物线C1或C2上是否存在一点Q，使得△EBQ的面积最大？若存在，求出Q的坐标和△EBQ面积的最大值；若不存在，请说明理由．
分析：（1）已知A、B、C、D四点坐标，利用待定系数法即可确定两函数的解析式．
（2）根据直线BE：y=
x-1知，该直线必过（0，-1）点，那么∠EBO=∠CBO，若以点P、B、C为顶点的△PBC与△BOE相似，那么夹这组对应角的对应边必成比例，先求出BC、BO、BE的长，然后分情况根据线段间的比例关系求出BP的长，进而得到OP的长，即可确定P点坐标．
（3）△EBQ中，BE长为定值，若以BE为底，当△EBQ的面积最大时，Q到直线BE的距离最大；由于点Q可能在抛物线C1或C2上，因此两种情况都要解一下，最后通过比较得到能使△EBQ面积最大的Q点．首先作直线l∥BE，分别令直线l与抛物线C1、C2有且仅有一个交点，那么符合条件的Q点必在这两个交点中，先求出这两个交点分别到直线BE的距离，距离大者符合条件，由此可得到Q点坐标和△EBQ的面积最大值．
（2）根据直线BE：y=
| 1 |
| 3 |
（3）△EBQ中，BE长为定值，若以BE为底，当△EBQ的面积最大时，Q到直线BE的距离最大；由于点Q可能在抛物线C1或C2上，因此两种情况都要解一下，最后通过比较得到能使△EBQ面积最大的Q点．首先作直线l∥BE，分别令直线l与抛物线C1、C2有且仅有一个交点，那么符合条件的Q点必在这两个交点中，先求出这两个交点分别到直线BE的距离，距离大者符合条件，由此可得到Q点坐标和△EBQ的面积最大值．
解答：解：（1）由于抛物线C1、C2都过点A（-3，0）、B（3，0），可设它们的解析式为：y=a（x-3）（x+3）；
抛物线C1还经过D（0，-3），则有：
-3=a（0-3）（0+3），a=
即：抛物线C1：y=
x2-3（-3≤x≤3）；
抛物线C2还经过C（0，1），则有：
1=a（0-3）（0+3），a=-
即：抛物线C2：y=-
x2+1（-3≤x≤3）．
（2）由于直线BE：y=
x-1必过（0，-1），所以∠CBO=∠EBO（tan∠CBO=tan∠EBO=
）；
由E点坐标可知：tan∠AOE≠
，即∠AOE≠∠CBO，所以它们的补角∠EOB≠∠CBx；
若以点P、B、C为顶点的△PBC与△BOE相似，只需考虑两种情况：
①∠CBP1=∠EBO，且OB：BE=BP1：BC，即：
3：
=BP1：
，得：BP1=
，OP1=OB-BP1=
；
∴P1（
，0）；
②∠P2BC=∠EBO，且BC：BP2=OB：BE，即：
：BP2=3：
，得：BP2=
，OP2=BP2-OB=
；
∴P2（-
，0）；
综上，符合条件的P点有：P1（
，0）、P2（-
，0）．
（3）如图，作直线l∥直线BE，设直线l：y=
x+b；
①当直线l与抛物线C1只有一个交点时：
x+b=
x2-3，即：x2-x-（3b+9）=0，
∴△=1+4（3b+9）=0，
解得，3b+9=-
，
∴x2-x+
=0
∴该交点Q2（
，-
）；
Q2到直线 BE：
x-y-1=0 的距离：
=
=
；
②当直线l与抛物线C2只有一个交点时：
x+b=-
x2+1，即：x2+3x+9b-9=0，
∴该交点Q1（-
，
）；
Q1到直线 BE：
x-y-1=0 的距离：
=
；
∴符合条件的Q点为Q1（-
，
）；
△EBQ的最大面积：Smax=
×BE×
=
．
方法二：
当点Q在C1上时，可设Q（x，
x2-3），过Q作QM平行y轴交BE于M，则M（m，
x-1），
则BM=
x-1-（
x2-3）=-
（x+0.5）2+
，所以当x=-0.5时BM最大值为
，
所以 S△EBQ最大=S△EQM+S△BQM=
（xB-xE）×
=0.5×5×
=
，
同理可得，Q在C 2上时，最大面积为
，
综上最大面积为
．
抛物线C1还经过D（0，-3），则有：
-3=a（0-3）（0+3），a=
| 1 |
| 3 |
即：抛物线C1：y=
| 1 |
| 3 |
抛物线C2还经过C（0，1），则有：
1=a（0-3）（0+3），a=-
| 1 |
| 9 |
即：抛物线C2：y=-
| 1 |
| 9 |
（2）由于直线BE：y=
| 1 |
| 3 |
| 1 |
| 3 |
由E点坐标可知：tan∠AOE≠
| 1 |
| 3 |
若以点P、B、C为顶点的△PBC与△BOE相似，只需考虑两种情况：
①∠CBP1=∠EBO，且OB：BE=BP1：BC，即：
3：
5
| ||
| 3 |
| 10 |
| 9 |
| 5 |
| 6 |
| 5 |
∴P1（
| 6 |
| 5 |
②∠P2BC=∠EBO，且BC：BP2=OB：BE，即：
| 10 |
5
| ||
| 3 |
| 50 |
| 9 |
| 23 |
| 9 |
∴P2（-
| 23 |
| 9 |
综上，符合条件的P点有：P1（
| 6 |
| 5 |
| 23 |
| 9 |
（3）如图，作直线l∥直线BE，设直线l：y=
| 1 |
| 3 |
①当直线l与抛物线C1只有一个交点时：
| 1 |
| 3 |
| 1 |
| 3 |
∴△=1+4（3b+9）=0，
解得，3b+9=-
| 1 |
| 4 |
∴x2-x+
| 1 |
| 4 |
∴该交点Q2（
| 1 |
| 2 |
| 35 |
| 12 |
Q2到直线 BE：
| 1 |
| 3 |
|
| ||||||
|
5
| ||
| 8 |
25
| ||
| 40 |
②当直线l与抛物线C2只有一个交点时：
| 1 |
| 3 |
| 1 |
| 9 |
∴该交点Q1（-
| 3 |
| 2 |
| 3 |
| 4 |
Q1到直线 BE：
| 1 |
| 3 |
|(-
| ||||||
|
27
| ||
| 40 |
∴符合条件的Q点为Q1（-
| 3 |
| 2 |
| 3 |
| 4 |
△EBQ的最大面积：Smax=
| 1 |
| 2 |
27
| ||
| 40 |
| 45 |
| 8 |
方法二：
当点Q在C1上时，可设Q（x，
| 1 |
| 3 |
| 1 |
| 3 |
则BM=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 25 |
| 12 |
| 25 |
| 12 |
所以 S△EBQ最大=S△EQM+S△BQM=
| 1 |
| 2 |
| 25 |
| 12 |
| 25 |
| 12 |
| 125 |
| 24 |
同理可得，Q在C 2上时，最大面积为
| 45 |
| 8 |
综上最大面积为
| 45 |
| 8 |
点评：考查了二次函数综合题．该题的难度和计算量都比较大，涉及了函数解析式的确定、相似三角形的判定和性质、图形面积的解法等重点知识；解答（2）题时，应注意分不同的对应边来进行讨论，以免漏解．（3）的难度较大，点到直线的距离公式【点（x0，y0）到直线（Ax+By+C=0）的距离为：d=
】是需要记住的内容．另外，题目在设计时结合了一定的生活元素，形式较为新颖．
| |Ax0+By0+C| | ||
|
练习册系列答案
相关题目
程“排水--清洗--灌水”中水量y（m3）与时间t（min）之间的函数图象．