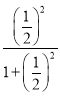Question

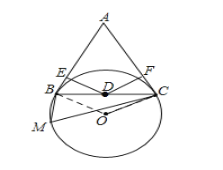
【题目】如图，已知BC是⊙O的弦，A是⊙O外一点，△ABC为正三角形，D为BC的中点，M为⊙O上一点．

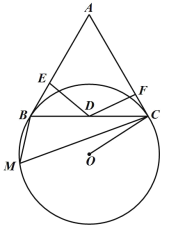
（1）若AB是⊙O的切线，求∠BMC；

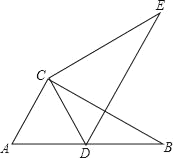
（2）在（1）的条件下，若E，F分别是AB，AC上的两个动点，且EDF120，⊙O的半径为2，试问BECF的值是否为定值？若是，求出这个定值；若不是，请说明理由．

Answer 1

【答案】（1）60°；（2）BE+CF的值是定值，BE+CF=.

【解析】

（1）连接BO，由AB是切线可以得到∠ABO的度数，由△ABC为等边三角形，得到∠OBC的度数，然后得到∠BOC，根据圆心角与圆周角的关系得到∠BMC的度数.

（2）作DH⊥AB于H，DN⊥AC于N，连结AD ，OD，如图2，根据等边三角形三角形的性质得AD平分∠BAC，∠BAC=60°，则利用角平分线性质得DH=DN，根据四边形内角和得∠HDN=120°，由于∠EDF=120°，所以∠HDE=∠NDF，接着证明△DHE≌△DNF得到HE=NF，于是BE+CF=BH+CN，再计算出BH=BD，CN=DC，则BE+CF=BC，于是可判断BE+CF的值是定值，为等边△ABC边长的一半，再计算BC的长即可．

（1）解：如图，连接BO，

∵AB是圆的切线，

∴∠ABO=90°，

∵△ABC是等边三角形，

∴∠ABC=60°，

∴∠CBO=90°-60°=30°，

∵BO=CO，

∴∠BCO=∠CBO=30°，

∴∠BOC=120°，

∴∠BMC=

（2）解：BE+CF的值是为定值．

理由：作DH⊥AB于H，DN⊥AC于N，连结AD，OD，如图2，

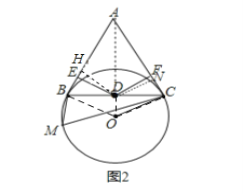
∵△ABC为正三角形，D为BC的中点，

∴AD平分∠BAC，∠BAC=60°，

∴DH=DN，∠HDN=120°，

∵∠EDF=120°，

∴∠HDE=∠NDF，

在△DHE和△DNF中，

∴，

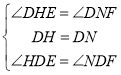∴△DHE≌△DNF，

∴HE=NF，

∴BE+CF=BH-EH+CN+NF=BH+CN，

在Rt△DHB中，∵∠DBH=60°，

∴BH=BD，

同理可得CN=OC，

∴BE+CF=DB+DC=BC，

∵BD=，

∴BC=，

∴BE+CF=，

∴BE+CF的值是定值，为：．