Question

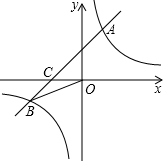已知，如图，在平面直角坐标系中，直线y=x+b与双曲线y=

k

x

(k≠0)交于A、B两点，与x轴交于C点，点A的坐标为（m，5），点B的坐标为（n，-2）．
（1）求该反比例函数和一次函数的解析式；
（2）在x轴上是否存在一点E，使得S_△BCE=

4

3

S_△BCO？若存在请求出点E的坐标；若不存在请说明理由．

Answer 1

考点：反比例函数与一次函数的交点问题

专题：计算题

分析：（1）将A与B坐标代入一次函数与反比例解析式，消去b与k得到关于m与n的方程组，求出方程组的解得到m与n的值，进而求出k与b的值，确定出一次函数与反比例解析式；
（2）存在，理由为：对于一次函数，令y=0求出x的值，确定出C坐标，得到OC的长，三角形BCO的面积由OC为底，B纵坐标的绝对值为高求出，进而根据题意确定出三角形BCE的面积，三角形BCE以CE为底，B纵坐标的绝对值为高，求出CE的长，即可确定出E的坐标．

解答：解：（1）将A（m，5），B（n，-2）分别代入一次函数得：m+b=5，n+b=-2，
整理得：m-n=7①；
将A（m，5），B（n，-2）分别代入反比例函数得：5=

k

m

，-2=

k

n

，
整理得：

n

m

=-

5

2

，即5m+2n=0②，
联立①②解得：m=2，n=-5，
∴k=10，b=3，
则一次函数解析式为y=x+3，反比例解析式为y=

10

x

；
（2）存在，
对于一次函数y=x+3，令y=0，得到x=-3，即OC=3，
∴S_△BCO=

1

2

OC•|y_B纵坐标|=3，
∴S_△BCE=

4

3

S_△BCO=4，即

1

2

CE•|y_B纵坐标|=4，
∴CE=4，又C（-3，0），
则E（-7，0）或（1，0）．

点评：此题考查了一次函数与反比例函数的交点问题，涉及的知识有：待定系数法求函数解析式，坐标与图形性质，一次函数与坐标轴的交点，以及三角形的面积求法，弄清题意是解本题的关键．