Question

【题目】小慧根据学习函数的经验，对函数图像与性质进行了探究，下面是小慧的探究过程，请补充完整：

（1）若，为该函数图像上不同的两点，则 ，该函数的最小值为 .

（2）请在坐标系中画出直线与函数的图像并写出当时的取值范围是 .

Answer 1

【答案】（1），；（2）作图见解析，或

【解析】

（1）将代入函数解析式，即可求得m，由可知；

（2）采用描点作图画出图象，再根据图象判断直线在函数图象下方时x的取值范围，即可得到时x的取值范围．

（1）将代入得：

，解得或-6

∵，为该函数图像上不同的两点

∴

∵

∴即函数的最小值为1，

故答案为：-6，1．

（2）当时，函数，

当时，函数

如图所示，

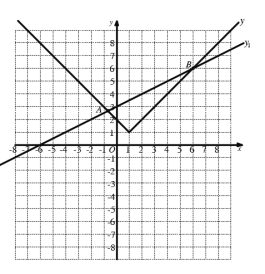
设y1与y的图像左侧交点为A，右侧交点为B

解方程组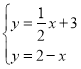得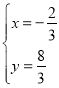，则A点坐标为，

解方程组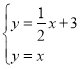得，则B点坐标为

观察图像可得：当直线在函数图象下方时，

x的取值范围为或，

所以当时的取值范围是或.

故答案为：或.