题目内容
 如图,A、B分别是反比例函数y=
如图,A、B分别是反比例函数y=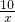 ,y=
,y= 图象上的点,过A、B作x轴的垂线,垂足分别为C、D,连接OB、OA,OA交BD于E点,△BOE的面积为S1,四边形ACDE的面积为S2,则S2-S1=________.
图象上的点,过A、B作x轴的垂线,垂足分别为C、D,连接OB、OA,OA交BD于E点,△BOE的面积为S1,四边形ACDE的面积为S2,则S2-S1=________.
2
分析:先根据A、B分别是反比例函数y=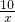 ,y=
,y= 图象上的点可知S△AOC=
图象上的点可知S△AOC= ×10=5,S△BOD=
×10=5,S△BOD= ×6=3,由函数图象可知,S2-S1=S△AOC-S△BOD,故可得出结论.
×6=3,由函数图象可知,S2-S1=S△AOC-S△BOD,故可得出结论.
解答:∵A、B分别是反比例函数y=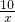 ,y=
,y= 图象上的点,
图象上的点,
∴S△AOC= ×10=5,S△BOD=
×10=5,S△BOD= ×6=3,
×6=3,
∴S2-S1=S△AOC-S△BOD=5-3=2.
故答案为:2.
点评:本题考查的是反比例函数系数k的几何意义,熟知在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是 是解答此题的关键.
是解答此题的关键.
分析:先根据A、B分别是反比例函数y=
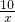 ,y=
,y= 图象上的点可知S△AOC=
图象上的点可知S△AOC= ×10=5,S△BOD=
×10=5,S△BOD= ×6=3,由函数图象可知,S2-S1=S△AOC-S△BOD,故可得出结论.
×6=3,由函数图象可知,S2-S1=S△AOC-S△BOD,故可得出结论.解答:∵A、B分别是反比例函数y=
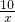 ,y=
,y= 图象上的点,
图象上的点,∴S△AOC=
 ×10=5,S△BOD=
×10=5,S△BOD= ×6=3,
×6=3,∴S2-S1=S△AOC-S△BOD=5-3=2.
故答案为:2.
点评:本题考查的是反比例函数系数k的几何意义,熟知在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是
 是解答此题的关键.
是解答此题的关键. 
练习册系列答案
相关题目
(12分)如图1,在平面上,给定了半径为 的⊙
的⊙ ,对于任意点
,对于任意点 ,在射线
,在射线 上取一点
上取一点 ,使得
,使得 ·
· =
= ,这种把点
,这种把点 变为点
变为点 的变换叫做反演变换,点
的变换叫做反演变换,点 与点
与点 叫做互为反演点,⊙
叫做互为反演点,⊙ 称为基圆.
称为基圆.

⑴如图2,⊙ 内有不同的两点
内有不同的两点 、
、 ,它们的反演点分别是
,它们的反演点分别是 、
、 ,则与∠
,则与∠ 一定相等的角是( ▲ )
一定相等的角是( ▲ )
⑵如图3,⊙ 内有一点
内有一点 ,请用尺规作图画出点
,请用尺规作图画出点 的反演点
的反演点 ;(保留画图痕迹,不必写画法).
;(保留画图痕迹,不必写画法).
⑶如果一个图形上各点经过反演变换得到的反演点组成另一个图形,那么这两个图形叫做互为反演图形.已知基圆 的半径为
的半径为 ,另一个半径为
,另一个半径为 的⊙
的⊙ ,作射线
,作射线 交⊙
交⊙ 于点
于点 、
、 ,点
,点 、
、 关于⊙
关于⊙ 的反演点分别是
的反演点分别是 、
、 ,点
,点 为⊙
为⊙ 上另一点,关于⊙
上另一点,关于⊙ 的反演点为
的反演点为 .求证:∠
.求证:∠ =90°.
=90°.
 的⊙
的⊙ ,对于任意点
,对于任意点 ,在射线
,在射线 上取一点
上取一点 ,使得
,使得 ·
· =
= ,这种把点
,这种把点 变为点
变为点 的变换叫做反演变换,点
的变换叫做反演变换,点 与点
与点 叫做互为反演点,⊙
叫做互为反演点,⊙ 称为基圆.
称为基圆.
⑴如图2,⊙
 内有不同的两点
内有不同的两点 、
、 ,它们的反演点分别是
,它们的反演点分别是 、
、 ,则与∠
,则与∠ 一定相等的角是( ▲ )
一定相等的角是( ▲ )A.∠ | B.∠ | C.∠ | D.∠ |
 内有一点
内有一点 ,请用尺规作图画出点
,请用尺规作图画出点 的反演点
的反演点 ;(保留画图痕迹,不必写画法).
;(保留画图痕迹,不必写画法).⑶如果一个图形上各点经过反演变换得到的反演点组成另一个图形,那么这两个图形叫做互为反演图形.已知基圆
 的半径为
的半径为 ,另一个半径为
,另一个半径为 的⊙
的⊙ ,作射线
,作射线 交⊙
交⊙ 于点
于点 、
、 ,点
,点 、
、 关于⊙
关于⊙ 的反演点分别是
的反演点分别是 、
、 ,点
,点 为⊙
为⊙ 上另一点,关于⊙
上另一点,关于⊙ 的反演点为
的反演点为 .求证:∠
.求证:∠ =90°.
=90°.
(12分)如图1,在平面上,给定了半径为 的⊙
的⊙ ,对于任意点
,对于任意点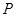 ,在射线
,在射线 上取一点
上取一点 ,使得
,使得 ·
· =
= ,这种把点
,这种把点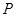 变为点
变为点 的变换叫做反演变换,点
的变换叫做反演变换,点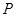 与点
与点 叫做互为反演点,⊙
叫做互为反演点,⊙ 称为基圆.
称为基圆.
⑴如图2,⊙ 内有不同的两点
内有不同的两点 、
、 ,它们的反演点分别是
,它们的反演点分别是 、
、 ,则与∠
,则与∠ 一定相等的角是( ▲ )
一定相等的角是( ▲ )
A.∠ | B.∠ | C.∠ | D.∠ |
 内有一点
内有一点 ,请用尺规作图画出点
,请用尺规作图画出点 的反演点
的反演点 ;(保留画图痕迹,不必写画法).
;(保留画图痕迹,不必写画法).⑶如果一个图形上各点经过反演变换得到的反演点组成另一个图形,那么这两个图形叫做互为反演图形.已知基圆
 的半径为
的半径为 ,另一个半径为
,另一个半径为 的⊙
的⊙ ,作射线
,作射线 交⊙
交⊙ 于点
于点 、
、 ,点
,点 、
、 关于⊙
关于⊙ 的反演点分别是
的反演点分别是 、
、 ,点
,点 为⊙
为⊙ 上另一点,关于⊙
上另一点,关于⊙ 的反演点为
的反演点为 .求证:∠
.求证:∠ =90°.
=90°.

 (C)∠
(C)∠ (D)∠
(D)∠
 =90°.
=90°.
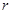 的⊙
的⊙ ,对于任意点
,对于任意点 ,在射线
,在射线 上取一点
上取一点 ,使得
,使得 =
= ,这种把点
,这种把点
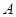 、
、 ,它们的反演点分别是
,它们的反演点分别是 、
、 ,则与∠
,则与∠ (C)∠
(C)∠ (D)∠
(D)∠ ,请用尺规作图画出点
,请用尺规作图画出点 ;(保留画图痕迹,不必写画法).
;(保留画图痕迹,不必写画法). 的⊙
的⊙ ,作射线
,作射线 交⊙
交⊙ =90°.
=90°.