题目内容
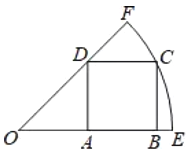
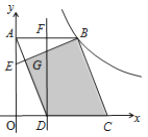
【题目】如图，在平面直角坐标系中，
为坐标原点，平行四边形
的边
在
轴正半轴上，顶点
在
轴正半轴上，函数
的图像经过点
，点
是线段
上接近点的三等分点，
，垂足为点
，且恰好是线段
的中点，连结
，
交于点
，则四边形
的面积是（）
A.
B.5C.
D.
【答案】C
【解析】
先证明△ADO≌△BCH，把所求面积进行转换，利用已知条件，把所构造的矩形面积计算出来，利用
，用排除法可以得到答案.
解：如图，过B点向x轴作垂线，交x轴于点H，
易知四边形AOHB是矩形，
∵
是平行四边形，
∴AD=BC，∠ADC=∠BCH，
又∵
，且
恰好是线段
的中点，
∴
，且AF=CH，
∴△ADO≌△BCH（SAS），
∴
（等量替换），
∴
由∵
，
，
选项B、C、D都大于等于5，因此排除，
故答案为A.
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
