题目内容

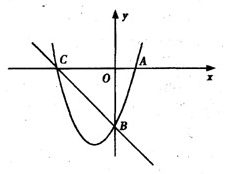
如图，已知抛物线y＝a(x－1)2＋(a≠0)经过点A(－2，0)，抛物线的顶点为D，过O作射线OM∥AD．过顶点D平行于轴的直线交射线OM于点C，B在轴正半轴上，连结BC．

（1）求该抛物线的解析式；
（2）若动点P从点O出发，以每秒1个长度单位的速度沿射线OM运动，设点P运动的时间为t（s）．问：当t为何值时，四边形DAOP分别为平行四边形？直角梯形？等腰梯形？
（3）若OC＝OB，动点P和动点Q分别从点O和点B同时出发，分别以每秒1个长度单位和2个长度单位的速度沿OC和BO运动，当其中一个点停止运动时另一个点也随之停止运动．设它们的运动的时间为t（s），连接PQ，当t为何值时，四边形BCPQ的面积最小？并求出最小值及此时PQ的长．

（1）y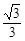＝－(x－1)2＋（2）当t＝6s、5s、4s时，四边形DAOP分别为平行四边形、直角梯形、等腰梯形．（3）t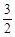＝（s）时，S四边形BCPQ的最小值为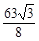，PQ的长为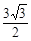

解析

练习册系列答案
相关题目

如图，已知抛物线ｙ＝ｘ－ａｘ＋ａ－4ａ－4与ｘ轴相交于点A和点B，与ｙ轴相交于点D（0，8），直线DC平行于ｘ轴，交抛物线于另一点C，动点P以每秒2个单位长度的速度从C点出发，沿C→D运动，同时，点Q以每秒1个单位长度的速度从点A出发，沿A→B运动，连接PQ、CB，设点P运动的时间为t秒．

（１）求ａ的值；

（２）当四边形ODPQ为矩形时，求这个矩形的面积；

（３）当四边形PQBC的面积等于14时，求t的值．

（４）当t为何值时，△PBQ是等腰三角形？
（9分）如图，已知抛物线y＝x2＋bx－3a过点A(1，0)，B(0，－3)，与x轴交于另一点C．

(1)求抛物线的解析式；
(2)若在第三象限的抛物线上存在点P，使△PBC为以点B为直角顶点的直角三角形，
求点P的坐标；
(3)在(2)的条件下，在抛物线上是否存在一点Q，使以P，Q，B，C为顶点的四边形
为直角梯形？若存在，请求出点Q的坐标；若不存在，请说明理由．

（本题9分）如图，已知抛物线y＝ax2＋bx＋3的图象与x轴交于A、B两点，与y轴交于点C，且点C、D是抛物线上的一对对称点．

【小题1】(1)求抛物线的解析式；
【小题2】(2)求点D的坐标，并在图中画出直线BD；
【小题3】(3)求出直线BD的一次函数解析式，并根据图象回答：当x满足什么条件时，上述二次函数的值大于该一次函数的值．

（9分）如图，已知抛物线y＝x2＋bx－3a过点A(1，0)，B(0，－3)，与x轴交于另一点C．

(1)求抛物线的解析式；
(2)若在第三象限的抛物线上存在点P，使△PBC为以点B为直角顶点的直角三角形，
求点P的坐标；
(3)在(2)的条件下，在抛物线上是否存在一点Q，使以P，Q，B，C为顶点的四边形
为直角梯形？若存在，请求出点Q的坐标；若不存在，请说明理由．

（本题满分10分）

如图，已知抛物线y＝ax2＋bx＋c(a≠0)的对称轴为x＝1，且抛物线经过A（—1，0）、C（0，—3）两点，与x轴交于另一点B．

1.（1）求这条抛物线所对应的函数关系式；

2.（2）在抛物线的对称轴x＝1上求一点M，使点M到点A的距离与到点C的距离之和最小，并求出此时点M的坐标；

3.（3）设点P为抛物线的对称轴x＝1上的一动点，求使∠PCB＝90°的点P的坐标．

 

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网