题目内容
【题目】如图，正方形ABCD的对角线长为8 
，E为AB上一点，若EF⊥AC于F，EG⊥BD于G，则EF+EG= ． 
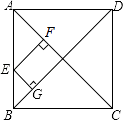
【答案】4 
【解析】解：如图：
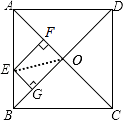
∵四边形ABCD是正方形，
∴OA=OB=4 ，
又∵S△ABO=S△AEO+S△EBO，
∴ 
OAOB= OAEF+ OBEG，
即 ×4 ×4 = ×4 ×（EF+EG）
∴EF+EG=4 ．
所以答案是：4 ．
【考点精析】掌握正方形的性质是解答本题的根本，需要知道正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．
练习册系列答案
相关题目
【题目】为了响应市委和市政府“绿色环保，节能减排”的号召，幸福商场用3300元购进甲、乙两种节能灯共计100只，很快售完．这两种节能灯的进价、售价如下表：
进价（元/只） | 售价（元/只） | |
甲种节能灯 | 30 | 40 |
甲种节能灯 | 35 | 50 |
（1）求幸福商场甲、乙两种节能灯各购进了多少只？
（2）全部售完100只节能灯后，商场共计获利多少元？
