题目内容
某商店购进一种商品，每件商品进价30元.试销中发现这种商品每天的销售量y(件)
与每件销售价x(元)的关系数据如下：
| x | 30 | 32 | 34 | 36 |
| y | 40 | 36 | 32 | 28 |
（1）已知y与x满足一次函数关系，根据上表，求出y与x之间的关系式（不写出自变量x的取值范围）；
（2）如果商店销售这种商品，每天要获得150元利润，那么每件商品的销售价应定为多少元？
（3）设该商店每天销售这种商品所获利润为w(元)，求出w与x之间的关系式，并求出每件商品销售价定为多少元时利润最大？
解：（1）设该函数的表达式为y=kx+b，根据题意，得
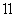
………………………2分
解得，
∴该函数的表达式为y= -2x+100 ………………3分
（2）根据题意，得，
（-2x+100）（x -30）=150 ………………４分
解这个方程得，
x1=35，x2=45 ………………6分
∴每件商品的销售价定为35元或45元时日利润为150元
…………………7分
（3）根据题意，得
w=(-2x+100)(x-30） …………………8分
= -2x2+160x-3000
= -2(x-40)2 +200
∵a= -2<0 则抛物线开口向下，函数有最大值
即当x=40时，w的值最大.
∴当销售单价为40元时获得利润最大.…
某校10名学生参加“心理健康”知识测试，他们得分情况如下表：
| 人数 | 2 | 3 | 4 | 1 |
| 分数 | 80 | 85 | 90 | 95 |
那么这10名学生所得分数的众数和中位数分别是 （ ）
A. 95和 85 B. 90和85 C. 90和87.5 D. 85和87.5
八年级（1）班学生在完成课题学习“体质健康测试中的数据分析”
后，利用课
外活动时间积极参加体育锻炼，每位同学从篮球、跳绳、立定跳远、长跑、铅球中选一项进行训练，训练后都进行了测试．现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图．
项目选择人数情况统计图 训练后篮球定时定点投篮测试进球数统计图
 | |||
 | |||
请你根据上面提供的信息回答下列问题：
（1）（3分）扇形图中跳绳部分的扇形圆心角为 度，该班共有学生 人，
训练后篮球定时定点投篮平均每个人的进球数是 ．
（2）（5分）老师决定从选择铅球训练的3名男生和1名女生中任选两名学生先进行测试，请用列表或画树形图的方法求恰好选中两名男生的概率．
，且a、b是两个连续的整数，则
.某中学数学兴趣小组为了解本校学生对电视节目的喜爱情况，随机调查了部分学生最喜爱哪一类节目 (被调查的学生只选一类并且没有不选择的) ,并将调查结果制成了如下的两个统计图（不完整）.请你根据图中所提供的信息，完成下列问题：
 |
（1）求本次调查的学生人数；
（2）请将两个统计图补充完整，并求出新闻节目在扇形统计图中所占圆心角的度数；
（3）若该中学有2000名学生，请估计该校喜爱电视剧节目的人数.
，3 C.3,4,8 D.4,5，6
的倒数为 
B.
C.