题目内容
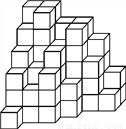
墙角处有若干个大小相同的小正方体堆成如图所示的立体图形,如果你打算搬走其中部分小正方体,但希望搬完后该立体图形的主视图、左视图和俯视图都不变,那么你最多可以搬走____个小正方体?
练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
题目内容
墙角处有若干个大小相同的小正方体堆成如图所示的立体图形,如果你打算搬走其中部分小正方体,但希望搬完后该立体图形的主视图、左视图和俯视图都不变,那么你最多可以搬走____个小正方体?

 华东师大版一课一练系列答案
华东师大版一课一练系列答案