题目内容
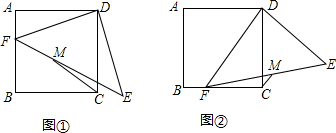
19.已知,四边形ABCD是正方形,点F是边AB、BC上一动点,DE⊥DF,且DE=DF,M为EF的中点.(1)当点F在边AB上时,(如图①).
①求证:点E在直线BC上;
②若BF=2,则MC的长为$\sqrt{2}$;
(2)当点F在BC上时,(如图②),求$\frac{BF}{CM}$的值.
分析 (1)①连接CE,证明△ADF≌△CDE,得到∠DCE=∠DAF=90°即可;
②作FK∥MC,证明CM=$\frac{1}{2}$FK,求出FK=$\sqrt{2}$BF即可;
(2)过点E作CD的平行线分别交AD、BC的延长线于K、Q,EN∥MC,根据平行线等分线段定理即可解答.
解答 解: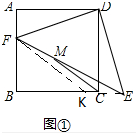 (1)①如图①,连接CE,
(1)①如图①,连接CE,
∵∠ADC=90°,DE⊥DF,
∴∠ADF=∠CDE,
在△ADF和△CDE中,
$\left\{\begin{array}{l}{AD=DC}\\{∠ADF=∠CDE}\\{DF=DE}\end{array}\right.$,
∴△ADF≌△CDE,
∴∠DCE=∠DAF=90°,
∴点E在直线BC上;
②如图①,作FK∥MC,∵M为EF的中点,
∴CM=$\frac{1}{2}$FK,
∵∠DMB=∠DCB=90°,
∴D、M、C、B四点共圆,
∴∠MCD=∠MBD=45°,
∴∠BKF=45°,
∵BF=2,∴FK=2$\sqrt{2}$,
∴CM=$\frac{1}{2}$FK=$\sqrt{2}$;
(2)过点E作CD的平行线分别交AD、BC的延长线于K、G,EN∥MC,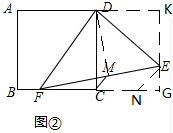
∵M为EF的中点,
∴CM=$\frac{1}{2}$NE,FC=CN,
∴NG=EG=BF,
$\frac{BF}{CM}$=$\frac{BF}{\frac{1}{2}NE}$=$\frac{BF}{\frac{1}{2}\sqrt{2}NG}$=$\sqrt{2}$.
点评 本题考查的是正方形的性质、全等三角形的判定和性质以及平行线分线段成比例定理,灵活运用性质和定理进行解答是解题的关键,注意辅助线的作法.

练习册系列答案
相关题目
14.下列分式一定有意义的是( )
| A. | $\frac{{x}^{2}+1}{{x}^{2}-1}$ | B. | $\frac{x+1}{x^2}$ | C. | $\frac{x-1}{{x}^{2}+1}$ | D. | $\frac{{x}^{2}}{x+1}$ |
11.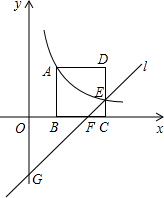 如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n,$\frac{2}{3}$),过点E的直线交x轴于点F,交y轴于点G(0,-2),则点F的坐标是( )
如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n,$\frac{2}{3}$),过点E的直线交x轴于点F,交y轴于点G(0,-2),则点F的坐标是( )
 如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n,$\frac{2}{3}$),过点E的直线交x轴于点F,交y轴于点G(0,-2),则点F的坐标是( )
如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n,$\frac{2}{3}$),过点E的直线交x轴于点F,交y轴于点G(0,-2),则点F的坐标是( )| A. | ($\frac{5}{4}$,0) | B. | ($\frac{7}{4}$,0) | C. | ($\frac{9}{4}$,0) | D. | ($\frac{11}{4}$,0) |
9.下列说法正确的是( )
| A. | 一个游戏的中奖率是1%,则做100次这样的游戏一定会中奖 | |
| B. | 一组数据6,8,7,9,7,10的众数和中位数都是7 | |
| C. | 为了解全国中学生的心理健康情况,应该采用全面调查的方式 | |
| D. | 若甲乙两人六次跳远成绩的方差S${\;}_{甲}^{2}$=0.1,S${\;}_{乙}^{2}$=0.03,则乙的成绩更稳定 |
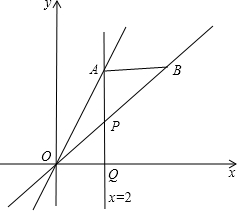 已知:直线y=2x与x=2相交于点A,直线x=2与x轴相交于点Q,点P是射线AQ上的一点,点B是直线OP上的一点,设AP=t,点B的坐标为(a,b).
已知:直线y=2x与x=2相交于点A,直线x=2与x轴相交于点Q,点P是射线AQ上的一点,点B是直线OP上的一点,设AP=t,点B的坐标为(a,b).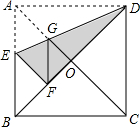 如图,在正方形纸片ABCD中,对角线AC,BD交于点O,折叠正方形ABCD使AD落在BD上,点A恰好与BD上的点F重合,展开后,折痕DE分别交AB,AC于点E、G,连接GF,有下列结论:①∠AGD=122.5°;②$\frac{AD}{AE}=2$;③BE=2OG;④DG=2EG;⑤AC-AD=EF,其中正确的序号是( )
如图,在正方形纸片ABCD中,对角线AC,BD交于点O,折叠正方形ABCD使AD落在BD上,点A恰好与BD上的点F重合,展开后,折痕DE分别交AB,AC于点E、G,连接GF,有下列结论:①∠AGD=122.5°;②$\frac{AD}{AE}=2$;③BE=2OG;④DG=2EG;⑤AC-AD=EF,其中正确的序号是( )


