题目内容
在直角坐标平面内，点O为坐标原点，二次函数y＝x2＋(k－5)x－(k＋4)的图象交x轴于点A(x1，0)、B(x2，0)，且(x1＋1)(x2＋1)＝－8．
(1)求二次函数的解析式；
(2)将上述二次函数图象沿x轴向右平移2个单位，设平移后的图象与y轴的交点为C，顶点为P，求△POC的面积．
答案：
解析：
解析：
|
(1)由题意知，xl、x2是方程x2＋(k－5)x－(k＋4)＝0的根，则x1＋x2＝5－k，x1·x2＝－(k＋4)，由(xl＋1)(x2＋1)＝－8，即x1·x2＋(x1＋x2)＝－9，得－(k＋4)＋(5－k)＝－9，解得k＝5，则所求二次函数的解析式为y＝x2－9. (2)由题意，平移后的图象的函数解析式为y＝(x－2)2－9，则点C的坐标为(0，－5)，顶点P的坐标为(2，－9)，所以△POC的面积S＝  ×5×2＝5.
|
练习册系列答案
阅读快车系列答案
相关题目
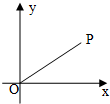如图，在直角坐标平面内，点P与原点O的距离OP=2，线段OP与x轴正半轴的夹角为30°，则点P的坐标是（ ）| A、（2，1） | ||
| B、（1，2） | ||
C、（
| ||
D、（1，
|
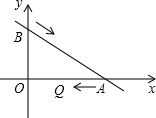如图，在直角坐标平面内，点0为坐标原点，直线AB经过A（8，0），B（0，6），现有两个动点P，Q．动点P从B沿BA方向以1个单位每秒的速度向A运动，动点Q从A沿AO方向2个单位每秒的速度向O运动，当P，Q两点中的任何一点到达终点时，运动停止．
如图，在直角坐标平面内，点P与原点O的距离OP=13，OP与x轴正半轴的夹角α的余弦值为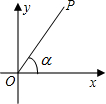
如图，在直角坐标平面内，点P与原点O的距离OP=3，线段OP与x轴正半轴的夹角为α，且