题目内容
在分式 的分子、分母同除以(x+1)可能为零的代数式,扩大了x的取值范围,请说明理由.
的分子、分母同除以(x+1)可能为零的代数式,扩大了x的取值范围,请说明理由.
解:由(x+1)(x-2)≠0,得x+1≠0,且x-2≠0,
所以x≠-1且x≠2.
当x≠-1且x≠2时,分式 有意义;
有意义;
当分式的分子、分母同除以(x+1)可能为零的代数式时,
①若x+1=0,原式=0,x的取值为全体实数.
②当x+1≠0时,原式可化为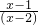 ,解得x≠2.
,解得x≠2.
故原分式的分子、分母同除以(x+1)可能为零的代数式,扩大了x的取值范围.
分析:先根据分式有意义的条件求出所给分式中x的取值范围,再把原分式的分子、分母同除以(x+1)求出x的取值范围,再把前后两次x的取值范围进行比较即可.
点评:此题比较简单,解答此题的关键是求出两次分式中未知数的值,再进行比较.
所以x≠-1且x≠2.
当x≠-1且x≠2时,分式
 有意义;
有意义;当分式的分子、分母同除以(x+1)可能为零的代数式时,
①若x+1=0,原式=0,x的取值为全体实数.
②当x+1≠0时,原式可化为
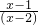 ,解得x≠2.
,解得x≠2.故原分式的分子、分母同除以(x+1)可能为零的代数式,扩大了x的取值范围.
分析:先根据分式有意义的条件求出所给分式中x的取值范围,再把原分式的分子、分母同除以(x+1)求出x的取值范围,再把前后两次x的取值范围进行比较即可.
点评:此题比较简单,解答此题的关键是求出两次分式中未知数的值,再进行比较.

练习册系列答案
相关题目