Question

已知点A（1，2），B（3，-5），P为x轴上一动点，求P到A、B的距离之差的绝对值最大时P点的坐标．

Answer 1

分析：易得当B′、A、P三点共线时，|PA-PB|最大，设直线AB′的解析式为y=kx+b，利用待定系数法即可求得直线AB′的解析式，点P即是此函数与x轴的交点坐标．

解答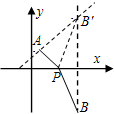：解：设B关于x轴的对称点为B′，连接PB′，AB′，则B′（3，5），PB′=PB，
∴|PA-PB|=|PA-PB′|≤AB′，
即B′、A、P三点共线时，|PA-PB|最大，
设直线AB′的解析式为为y=kx+b，则

2=k+b 5=3k+b

，
解得

k= 3 2 b= 1 2

，
∴直线AB′的解析式为y=

3

2

x+

1

2

；
由

y= 3 2 x+ 1 2 y=0

，
解得：

x=- 1 3 y=0

，
∴符合题意的点P为（ -

1

3

，0）．

点评：此题考查了待定系数法求一次函数的解析式以及三角形的三边关系等知识．此题难度适中，注意掌握辅助线的作法，注意数形结合思想的应用．