题目内容
13、抛物线y=a（x-2）2-2的图象如图所示，则它关于y轴对称的抛物线的解析式为y=2（x+2）2-2
．分析：将点（1，0）代入y=a（x-2）2-2中先求a，可知原抛物线顶点坐标为（2，-2），则它关于y轴对称的抛物线顶点坐标为（-2，-2），由此可求新抛物线的解析式．
解答：解：将点（1，0）代入y=a（x-2）2-2中，得a-2=0，
解得a=2，
又原抛物线顶点坐标为（2，-2），
∴它关于y轴对称的抛物线顶点坐标为（-2，-2），
∴新抛物线的解析式为y=2（x+2）2-2．
故本题答案为：y=2（x+2）2-2．
解得a=2，
又原抛物线顶点坐标为（2，-2），
∴它关于y轴对称的抛物线顶点坐标为（-2，-2），
∴新抛物线的解析式为y=2（x+2）2-2．
故本题答案为：y=2（x+2）2-2．
点评：本题考查了抛物线的轴对称与抛物线解析式的关系．关键是明确轴对称前后顶点坐标的变化规律．
练习册系列答案
新课标阶梯阅读训练系列答案
口算心算速算应用题系列答案
相关题目
A和C，和x轴的另一个交点为B．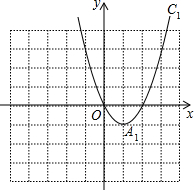
已知抛物线C1：y=x2-2x的图象如图所示，把C1的图象沿y轴翻折，得到抛物线C2的图象，抛物线C1与抛物线C2的图象合称图象C3．