Question

【题目】如图，菱形ABCD的边长为2，∠ABC=60°，E是AD的中点，点P是对角线BD上的动点，当AP+PE的值最小时，PC的长是（ ）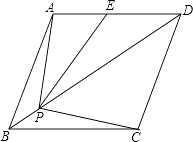

A.
B.2
C.
D.

Answer 1

【答案】C
【解析】如图所示，

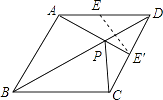
作点E关于直线BD的对称点E′，连接AE′，则线段AE′的长即为AP+PE的最小值，

∵菱形ABCD的边长为2，E是AD边中点，

∴DE=DE′= AD=1，

∴△AE′D是直角三角形，

∵∠ABC=60°，

∴∠PDE′= ∠ADC=30°，

∴PE′=DE′tan30°= ，

∴PC= = = ．

所以答案是：C．

【考点精析】认真审题，首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2)，还要掌握菱形的性质(菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半)的相关知识才是答题的关键．