题目内容
12+(1×2)2+22=(1×2+1)2;
22+(2×3)2+32=(2×3+1)2;
32+(3×4)2+42=(3×4+1)2;
(1)写出第2008个式子;
(2)利用计算器求第199个式子的值.
22+(2×3)2+32=(2×3+1)2;
32+(3×4)2+42=(3×4+1)2;
(1)写出第2008个式子;
(2)利用计算器求第199个式子的值.
分析:(1)观察不难发现,从1开始的两个连续自然数的平方和加上它们乘积的平方,等于这两个数的乘积与1的和的平方,然后写出第2008个式子即可;
(2)根据算式进行计算即可得解.
(2)根据算式进行计算即可得解.
解答:解:(1)∵12+(1×2)2+22=(1×2+1)2,
22+(2×3)2+32=(2×3+1)2,
32+(3×4)2+42=(3×4+1)2,
…,
∴第2008个式子为:20082+(2008×2009)2+20092=(2008×2009+1)2;
(2)1992+(199×200)2+2002,
=(199×200+1)2,
=39 8012,
=1 584 119 601.
22+(2×3)2+32=(2×3+1)2,
32+(3×4)2+42=(3×4+1)2,
…,
∴第2008个式子为:20082+(2008×2009)2+20092=(2008×2009+1)2;
(2)1992+(199×200)2+2002,
=(199×200+1)2,
=39 8012,
=1 584 119 601.
点评:本题是对数字变化规律的考查,比较简单,观察出两个数的组合方法是解题的关键.

练习册系列答案
相关题目
直角三角形两直角边长度为5,12,则斜边上的高( )
| A、6 | ||
| B、8 | ||
C、
| ||
D、
|
关于x的一元二次方程(a-1)x2+a2-1=0的一个根是x=0,则a等于( )
| A、1 | ||
| B、-1 | ||
| C、±1 | ||
D、
|
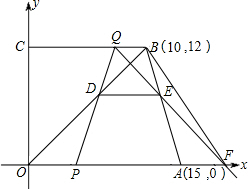 动时间为t(单位:秒).
动时间为t(单位:秒).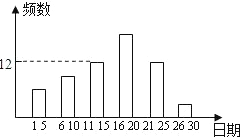 出一张卡片,抽到第四组作品的概率是多少?
出一张卡片,抽到第四组作品的概率是多少?