题目内容
如图1,已知抛物线y=-x2+bx+c经过点A(1,0),B(-3,0)两点,且与y轴交于点C.
(1) 求b,c的值。
(2)在第二象限的抛物线上,是否存在一点P,使得△PBC的面积最大?求出点P的坐标及△PBC的面积最大值.若不存在,请说明理由.
(3) 如图2,点E为线段BC上一个动点(不与B,C重合),经过B、E、O三点的圆与过点B且垂直于BC的直线交于点F,当△OEF面积取得最小值时,求点E坐标.
(1) 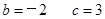 ;(2)点P坐标为(
;(2)点P坐标为(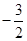 ,
,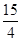 ),
),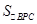 最大=
最大=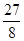 ;(3)
;(3)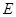 (
(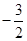 ,
,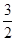 ) .
) .
解析试题分析:(1)将A、B两点坐标代入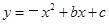 即可求出
即可求出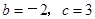 ;
;
(2)假设存在一点P(x,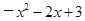 ),则△PBC的面积可表示为
),则△PBC的面积可表示为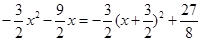 .从而可求出△PBC的面积最大值及点P的坐标;
.从而可求出△PBC的面积最大值及点P的坐标;
(3)根据题意易证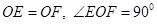 ,所以
,所以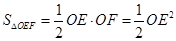 ,当OE最小时,△OEF面积取得最小值,点E在线段BC上, 所以当OE⊥BC时,OE最小此时点E是BC中点,因此 E(
,当OE最小时,△OEF面积取得最小值,点E在线段BC上, 所以当OE⊥BC时,OE最小此时点E是BC中点,因此 E(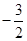 ,
,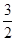 ) .
) .
试题解析:(1) b=-2,c=" 3"
(2)存在。理由如下:
设P点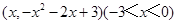
∵
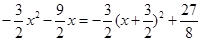
当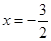 时, ∴
时, ∴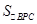 最大=
最大=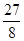
当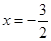 时,
时,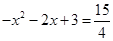
∴点P坐标为(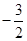 ,
,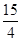 )
)
(3)∵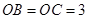 ∴
∴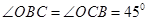 ,而
,而 ,
, 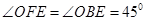 ,
,
∴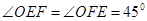 , ∴
, ∴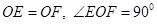
∴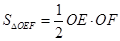
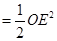
∴当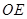 最小时,
最小时,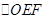 面积取得最小值.
面积取得最小值.
∵点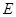 在线段
在线段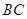 上, ∴当
上, ∴当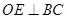 时,
时,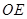 最小.
最小.
此时点E是BC中点
∴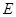 (
(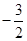 ,
,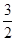 ).
).

练习册系列答案
相关题目
中秋节期间某水库养殖场为适应市场需求,连续用20天时间,采用每天降低水位以减少捕捞成本的办法,对水库中某种鲜鱼进行捕捞、销售.
九(1)班数学建模兴趣小组根据调查,整理出第x天( )的捕捞与销售的相关信息如下:
)的捕捞与销售的相关信息如下:
| 鲜鱼销售单价(元/kg) | 20 |
| 单位捕捞成本(元/kg) |  |
| 捕捞量(kg) | 950-10x |
(2)假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出,求第x天的收入y(元)与x(元)之间的函数关系式;(当天收入=日销售额
 日捕捞成本)
日捕捞成本)(3)试说明(2)中的函数y随x的变化情况,并指出在第几天y取得最大值,最大值是多少?
 为边长是
为边长是 的等边三角形,四边形
的等边三角形,四边形 为边长是6的正方形. 现将等边
为边长是6的正方形. 现将等边 与点
与点 重合,点
重合,点 、
、 、
、 在同一条直线上,
在同一条直线上, 方向向右匀速运动,当点
方向向右匀速运动,当点 秒(
秒( ).
).
 ,请直接写出
,请直接写出 与点
与点 重合时,作
重合时,作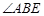 的角平分线
的角平分线 交
交 于点
于点 ,将
,将 绕点
绕点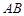 与边
与边 重合,得到
重合,得到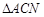 . 在线段
. 在线段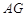 上是否存在
上是否存在 点,使得
点,使得 为等腰三角形. 如果存在,求线段
为等腰三角形. 如果存在,求线段 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由. 个单位长度,其余条件保持不变.
个单位长度,其余条件保持不变.  点从
点从 以每秒
以每秒 个单位长度开始移动,
个单位长度开始移动, 交折线
交折线 于
于 点,则当
点,则当 时,求
时,求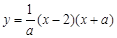
 与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.
与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.
 ).
).
 若在国外销售,平均每件产品的利润y2(元)与国外的销售数量t(千件)的关系为:
若在国外销售,平均每件产品的利润y2(元)与国外的销售数量t(千件)的关系为: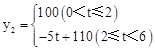
 .
. ?
?
 (n为正整数,且0<a1<a2<…<an)与x轴的交点为An-1(bn-1,0)和An(bn,0),当n=1时,第1条抛物线
(n为正整数,且0<a1<a2<…<an)与x轴的交点为An-1(bn-1,0)和An(bn,0),当n=1时,第1条抛物线 与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推.
与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推.