题目内容
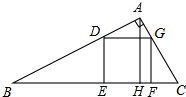 已知,如图,在Rt△ABC中,∠BAC=90°,四边形EFGD是正方形,点E、F在BC上,点D、G分别在AB、AC边上,且BE=4,FC=1,AH是△ABC的高.
已知,如图,在Rt△ABC中,∠BAC=90°,四边形EFGD是正方形,点E、F在BC上,点D、G分别在AB、AC边上,且BE=4,FC=1,AH是△ABC的高.(1)求EF的长;
(2)求AH的长.
考点:相似三角形的判定与性质
专题:常规题型
分析:(1)设正方形的边长为x,再根据相似三角形的判定定理得出△BDE∽△GCF,求出x的值,进而可得出结论.
(2)分别求HF和EH的值,可以求出CH和BH的值,即可求出AH的值.
(2)分别求HF和EH的值,可以求出CH和BH的值,即可求出AH的值.
解答:解:(1)设正方形的边长为x,
∵四边形DGFE是正方形,AH⊥BC,
∴AH⊥DE,
∵AH是△ABC的高,
∴∠CAH=∠B,
∴△BDE∽△GCF,
∴
=
即
=
,
EF=2;
(2)∵
=
,
=
,
∴
=
,∵EF=EH+FH=2,
解得:HF=
,
∴AH=
.
∵四边形DGFE是正方形,AH⊥BC,
∴AH⊥DE,
∵AH是△ABC的高,
∴∠CAH=∠B,
∴△BDE∽△GCF,
∴
| CF |
| FG |
| DE |
| BE |
| 1 |
| x |
| x |
| 4 |
EF=2;
(2)∵
| DE |
| AH |
| BE |
| EH |
| FG |
| AH |
| CF |
| CH |
∴
| BE |
| EH |
| CF |
| CH |
解得:HF=
| 2 |
| 5 |
∴AH=
| 7 |
| 5 |
点评:本题考查的是相似三角形的判定与性质,熟知相似三角形的对应边成比例是解答此题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
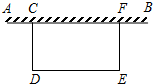 如图,某校广场有一段25米差个的旧围栏,现打算利用该围栏的一部分(或全部)为一边,围成一块100平方米的长方形草坪(如图CDEF,CD<CF)已知整修旧围栏的价格是每米1.75元,建新围栏的价格是4.5元.若CF=x米,计划修建费为y元.
如图,某校广场有一段25米差个的旧围栏,现打算利用该围栏的一部分(或全部)为一边,围成一块100平方米的长方形草坪(如图CDEF,CD<CF)已知整修旧围栏的价格是每米1.75元,建新围栏的价格是4.5元.若CF=x米,计划修建费为y元. 如图,在直角坐标系中,正方形ABCD的顶点B在x轴上,顶点C在y轴上,若AB=2,∠CBO=30°,试写出顶点A、B的坐标.
如图,在直角坐标系中,正方形ABCD的顶点B在x轴上,顶点C在y轴上,若AB=2,∠CBO=30°,试写出顶点A、B的坐标. 如图,A、B、C、D为矩形的四个顶点,AB=16cm,BC=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,点Q以2cm/s的速度向点D移动.当点P运动到点B停止时,点Q也随之停止运动.
如图,A、B、C、D为矩形的四个顶点,AB=16cm,BC=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,点Q以2cm/s的速度向点D移动.当点P运动到点B停止时,点Q也随之停止运动.