��Ŀ����
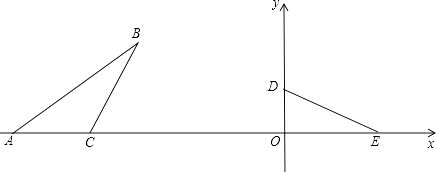
����Ŀ����ͼ����֪���κ���ͼ��Ķ�����ԭ�㣬ֱ��y= ![]() x+4��ͼ����ö��κ�����ͼ���ڵ�A��m��8����ֱ����x��Ľ���ΪC����y��Ľ���ΪB��
x+4��ͼ����ö��κ�����ͼ���ڵ�A��m��8����ֱ����x��Ľ���ΪC����y��Ľ���ΪB��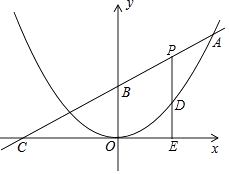
��1����������κ����Ľ���ʽ��B�����ꣻ
��2��PΪ�߶�AB�ϵ�һ�����㣨��P��A��B���غϣ�����P��x��Ĵ�����������κ�����ͼ��Ľ��ڵ�D����x�ύ�ڵ�E�����߶�PD��Ϊh����P�ĺ�����Ϊt����h��t֮��ĺ�����ϵʽ����д���Ա���t��ȡֵ��Χ��
��3���ڣ�2���������£����߶�AB���Ƿ���ڵ�P��ʹ���Ե�P��E��BΪ�����������Ϊ���������Σ������ڣ���ֱ��дP�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺�ߵ�A��m��8����ֱ��y= ![]() x+4�ϣ�
x+4�ϣ�
�� ![]() m+4=8�����m=8��
m+4=8�����m=8��
��A��8��8����
�������߹�ԭ�㣬
�������κ����Ľ���ʽΪy=ax2��a��0����
��A��8��8����y=ax2ͼ���ϣ�
��8=a��82�����a= ![]() ��
��
����κ����Ľ���ʽΪy= ![]() x2��
x2��
��ֱ��y=x+4��y�ύ�ڵ�B��
����x=0ʱ�ɵ�y=4����B��0��4��
��2��
�⣺��P����y= ![]() x+4�ϣ��Һ�����Ϊt��
x+4�ϣ��Һ�����Ϊt��
��P��t�� ![]() t+4����
t+4����
��PD��X����E��
��D��t�� ![]() ����E��t��0����
����E��t��0����
��PD=h=PE��DE=�� ![]() t+4����
t+4���� ![]() ��
��
��h=�� ![]() +
+ ![]() t+4��
t+4��
��P��A��B���غ������߶��ϣ�
��0��t��8��
��h��t�ĺ�����ϵʽΪh=�� ![]() +
+ ![]() t+4��0��t��8��
t+4��0��t��8��
��3��
�⣺��E��n��0����0��n��8������P��n�� ![]() n+4������B��0��4����
n+4������B��0��4����
��PB= ![]() =
= ![]() n��PE=
n��PE= ![]() n+4��BE=
n+4��BE= ![]() =
= ![]() ��
��
����PEB��������������PB=PE��PB=BE��PE=BE���������
�� ��PB=PEʱ������ ![]() n=
n= ![]() n+4�����n=2
n+4�����n=2 ![]() +2����ʱP������Ϊ��2
+2����ʱP������Ϊ��2 ![]() +2��
+2�� ![]() +5����
+5����
�ڵ�PB=BEʱ������ ![]() n=
n= ![]() �����n=8����ʱP��A�غϣ��������⣬��ȥ����n=��8��0��ȥ��
�����n=8����ʱP��A�غϣ��������⣬��ȥ����n=��8��0��ȥ��
�۵�PE=BEʱ������ ![]() n+4=
n+4= ![]() �����n=0����ȥ����n=
�����n=0����ȥ����n= ![]() ����ʱP������Ϊ��
����ʱP������Ϊ�� ![]() ��
�� ![]() ����
����
���Ͽ�֪��������������P�㣬������Ϊ��2 ![]() +2��
+2�� ![]() +5����
+5���� ![]() ��
�� ![]() ��
��
����������1����A���������ֱ�߽���ʽ�������m��ֵ�������A�����꣬���ô���ϵ��������������߽���ʽ�����ֱ�߽���ʽ�����B�����ꣻ��2����ֱ�ߺ������߽���ʽ�ɷֱ���t��ʾ��P��D�����꣬��ɱ�ʾ��PD�ij������ҵ�h��t�Ĺ�ϵʽ���ɵ�P���߶�AB�Ͽ�ȷ����t��ȡֵ��Χ����3������E������Ϊ��n��0���������n��ʾ��P�����꣬�Ӷ��ɱ�ʾ��PB��PE��BE�ij��ȣ�����PEBΪ����������ʱ������PB=PE��PB=BE��PE=BE����������ֱ�ɵõ�����n�ķ��̣������n��ֵ��������P�����꣮
�����㾫�����������⣬������Ҫ�˽���κ�����ͼ��(���κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ��)����Ҫ���ն��κ���������(�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С)�����֪ʶ���Ǵ���Ĺؼ���

 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�