题目内容
如图,在 中,
中, ,
, ,斜边
,斜边 的垂直平分线与
的垂直平分线与 的平分线都交
的平分线都交 于
于 点,则点
点,则点 到斜边
到斜边 的距离为 .
的距离为 .

【答案】
5
【解析】
试题分析:先根据斜边 的垂直平分线可得AD=BD,则∠DAB=∠DBA,根据AD平分
的垂直平分线可得AD=BD,则∠DAB=∠DBA,根据AD平分 可得∠CAD=∠DAB,再有
可得∠CAD=∠DAB,再有 结合三角形的内角和为180°即可求得∠CAD=30°,根据含30°角的直角三角形的性质可得AD=BD=2CD,从而可以求得CD的长,再根据角平分线的性质即可求得结果.
结合三角形的内角和为180°即可求得∠CAD=30°,根据含30°角的直角三角形的性质可得AD=BD=2CD,从而可以求得CD的长,再根据角平分线的性质即可求得结果.
∵斜边 的垂直平分线与
的垂直平分线与 的平分线都交
的平分线都交 于
于 点,
点,
∴AD=BD,∠CAD=∠DAB,
∴∠DAB=∠DBA,
∵ ,
,
∴∠CAD=∠DAB=∠DBA=30°,
∴AD=BD=2CD,
∵ ,
,
∴CD=5
∴点 到斜边
到斜边 的距离为5.
的距离为5.
考点:本题考查的是垂直平分线的性质,角平分线的性质
点评:解答本题的关键是熟练掌握垂直平分线的性质:垂直平分线上的点到线段两端的距离相等;角平分线的性质:角平分线上的点到角两边的距离相等.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 中,
中, ,
, 是斜边
是斜边 上的中线,
上的中线, ,
, ,点
,点 是
是 ,交
,交 延长线于点
延长线于点 ,
, .
.
 关于
关于 的函数关系式及定义域;(4分)
的函数关系式及定义域;(4分) ,当
,当 时,求
时,求 的长;(4分)
的长;(4分) 作
作 交
交 于
于 ,当
,当 和
和 相似时,求
相似时,求 的值.(6分)
的值.(6分) 中,
中, ,
, ,斜边
,斜边 的垂直平分线与
的垂直平分线与 的平分线都交
的平分线都交 于
于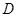 点,则点
点,则点
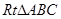 中,
中,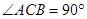 ,
, 是斜边
是斜边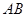 上的中线,
上的中线,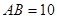 ,
,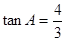 ,点
,点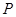 是
是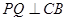 ,交
,交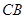 延长线于点
延长线于点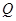 ,
,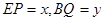 .
.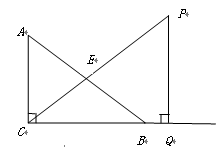
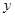 关于
关于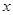 的函数关系式及定义域;(4分)
的函数关系式及定义域;(4分)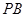 ,当
,当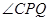 时,求
时,求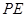 的长;(4分)
的长;(4分)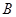 作
作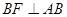 交
交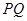 于
于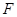 ,当
,当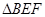 和
和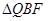 相似时,求
相似时,求 的值.(6分)
的值.(6分)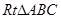 中,
中,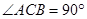 ,
, 是斜边
是斜边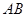 上的中线,
上的中线,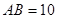 ,
,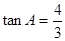 ,点
,点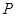 是
是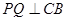 ,交
,交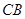 延长线于点
延长线于点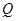 ,
, .
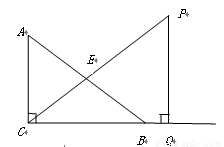
.
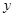 关于
关于 的函数关系式及定义域;(4分)
的函数关系式及定义域;(4分)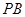 ,当
,当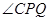 时,求
时,求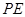 的长;(4分)
的长;(4分)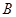 作
作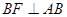 交
交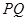 于
于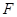 ,当
,当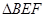 和
和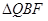 相似时,求
相似时,求