题目内容
如图,矩形ABCD的顶点A坐标为(0,0),顶点B的坐标是(-2,1),顶点C在y轴上.
(1)求点D的坐标;
(2)将矩形ABCD绕点O顺时针旋转,使点D落在x轴的点G处,得到矩形AEFG,EF与AD交于点H.过点H的反比例函数图象交FG于点I.求△AHI的面积;
(3)小明猜想△AHI是一个直角三角形,他的猜想对吗?请谈谈你的看法.
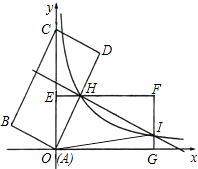
(1)求点D的坐标;
(2)将矩形ABCD绕点O顺时针旋转,使点D落在x轴的点G处,得到矩形AEFG,EF与AD交于点H.过点H的反比例函数图象交FG于点I.求△AHI的面积;
(3)小明猜想△AHI是一个直角三角形,他的猜想对吗?请谈谈你的看法.

(1)过B,D作△ABC和△ACD的高BM,DN,
在△ABC和△ACD中,
,
∴△ABC≌△ACD,
∴BM=DN=2,
过点B,D作x轴的垂线BP,DQ,则OP=AQ=2.
∵∠BAD=90°,
∴∠BAP+∠DAQ=90°,
又∵∠BAP+∠ABP=90°,
∴∠BAP=∠ADQ,
∴△OBP∽△DAQ,
∴
=
,
即
=
,
∴DQ=4,
则D的坐标是(2,4).
(2)(3)设直线OD的解析式是y=kx,把(2,4)代入解得k=2,
因而函数解析式是y=2x,
在直角△OBP中,根据勾股定理得到OB=
,
∴OE=OB=
,
即H点的纵坐标是
,
把y=
代入y=2x,得到x=
,
则H点的坐标是(
,
),
设反比例函数的解析式是y=
,把H点的坐标(
,
)代入解得k=
,
则解析式是y=
,
在直角△ADQ中,根据勾股定理得到OD=
=2
,
∴OG=OD=2
,
则I点的横坐标是2
,
把x=2
代入解析式得到y=
,
则I点的坐标是(2
,
),
∴OH2=
,OI2=
HI2=
,
∵
+
=
,
即AH2+HI2=AI2,
∴△AHI是一个直角三角形,
∴△AHI的面积是
•
÷2=
.

在△ABC和△ACD中,
|
∴△ABC≌△ACD,
∴BM=DN=2,
过点B,D作x轴的垂线BP,DQ,则OP=AQ=2.
∵∠BAD=90°,
∴∠BAP+∠DAQ=90°,
又∵∠BAP+∠ABP=90°,
∴∠BAP=∠ADQ,
∴△OBP∽△DAQ,
∴
| BP |
| AQ |
| OP |
| DQ |
即
| 1 |
| 2 |
| 2 |
| DQ |
∴DQ=4,
则D的坐标是(2,4).
(2)(3)设直线OD的解析式是y=kx,把(2,4)代入解得k=2,
因而函数解析式是y=2x,
在直角△OBP中,根据勾股定理得到OB=
| 5 |
∴OE=OB=
| 5 |
即H点的纵坐标是
| 5 |
把y=
| 5 |
| ||
| 2 |
则H点的坐标是(
| ||
| 2 |
| 5 |
设反比例函数的解析式是y=
| k |
| x |
| ||
| 2 |
| 5 |
| 5 |
| 2 |
则解析式是y=
| 5 |
| 2x |
在直角△ADQ中,根据勾股定理得到OD=
| OQ2+DQ2 |
| 5 |
∴OG=OD=2
| 5 |
则I点的横坐标是2
| 5 |
把x=2
| 5 |
| ||
| 4 |
则I点的坐标是(2
| 5 |
| ||
| 4 |
∴OH2=
| 25 |
| 4 |
| 325 |
| 16 |
| 225 |
| 16 |
∵
| 25 |
| 4 |
| 225 |
| 16 |
| 325 |
| 16 |
即AH2+HI2=AI2,
∴△AHI是一个直角三角形,
∴△AHI的面积是
|
|
| 75 |
| 16 |


练习册系列答案
相关题目






