题目内容
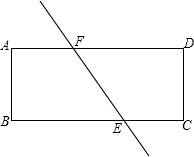
如图，直线a∥b，直线c与a、b相交，若∠1=45°，则∠2等于
- A.155°
- B.145°
- C.135°
- D.125°
C
分析：根据对顶角相等求出∠1的对顶角的度数，再根据两直线平行，同旁内角互补的性质列式即可求出∠2的度数．
解答：
解：如图，∵∠1=45°，
∴∠3=∠1=45°，
∵a∥b，
∴∠2=180°-∠3=180°-45°=135°．
故选C．
点评：本题考查了对顶角相等的性质，两直线平行，同旁内角互补的性质，熟记性质是解题的关键．
分析：根据对顶角相等求出∠1的对顶角的度数，再根据两直线平行，同旁内角互补的性质列式即可求出∠2的度数．
解答：
解：如图，∵∠1=45°，∴∠3=∠1=45°，
∵a∥b，
∴∠2=180°-∠3=180°-45°=135°．
故选C．
点评：本题考查了对顶角相等的性质，两直线平行，同旁内角互补的性质，熟记性质是解题的关键．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
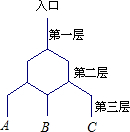如图所示是在竖直平面内的一个“通道游戏”．图中竖直线段和斜线段都表示通道，并且在交点处相遇，若竖直线段有一条的为第一层，有二条的为第二层，依此类推，现有一颗小弹子从第一层的通道里向下运动．并且小弹子落入每一条通道的可能性相同，则该小弹子从第三层通道的出口B脱出的概率为
